超球面,也稱n維球面,是普通的球面在任意維度的推廣。它是(n + 1)維空間內的n維流形。特別地,0維球面就是直線上的兩個點,1維球面是平面上的圓,2維球面是三維空間內的普通球面。高於2維的球面有時稱為超球面。
基本介紹
- 中文名:超球面
- 外文名:Hypersphere
- 定義:高於2維的球面
- 領域:數理科學
- 別稱:n維球面
超球面介紹

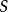
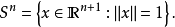
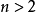

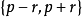
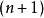
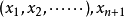

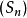
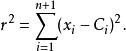
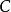


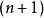



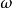
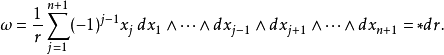
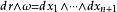
超球體體積



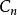
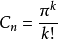
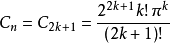
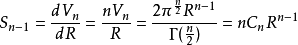
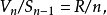
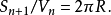

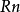
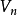
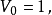
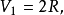

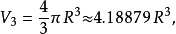
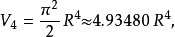
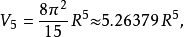
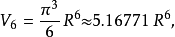
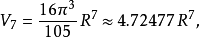
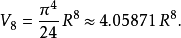

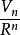
超球坐標系
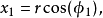
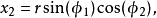
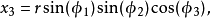
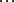
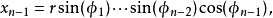

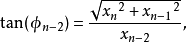

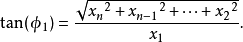
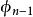
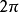
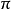

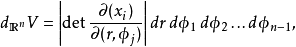
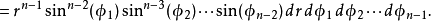

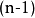
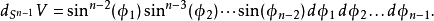
超球面,也稱n維球面,是普通的球面在任意維度的推廣。它是(n + 1)維空間內的n維流形。特別地,0維球面就是直線上的兩個點,1維球面是平面上的圓,2維球面是三維空間內的普通球面。高於2維的球面有時稱為超球面。

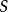
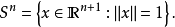
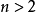

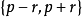
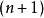
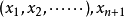

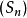
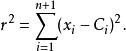
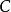


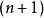



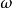
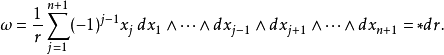
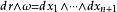



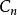
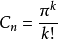
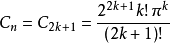
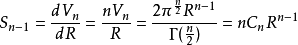
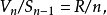
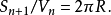

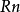
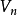
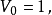
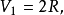

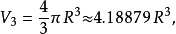
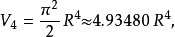
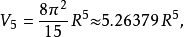
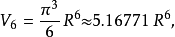
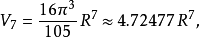
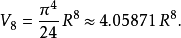

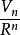
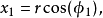
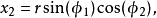
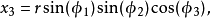
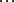
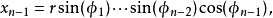
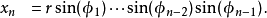

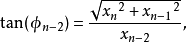

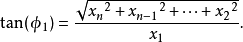
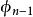
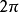
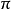

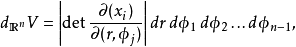
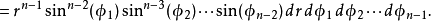

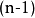
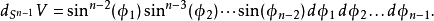
超球面,也稱n維球面,是普通的球面在任意維度的推廣。它是(n + 1)維空間內的n維流形。特別地,0維球面就是直線上的兩個點,1維球面是平面上的圓,2維球面是...
超球微分方程(hyperspherical equation)是數學物理中常見的常微分方程之一。連帶勒讓德方程經因變數變換後,可以得到超球微分方程;勒讓德方程和格根鮑爾方程都是它...
任何過球心的平面都把它分成兩個相等的半球面。過球心的任何兩個相交平面都將球體細分為四個球面二角形,其頂點全部與位於平面交線上的對徑點重合。...
n維球面是普通的球面在任意維度的推廣。它是(n + 1)維空間內的n維流形。...... 映射到二維平面上一樣,一個n維球面也可以通過球極平面投影的n維形式映射到n維...
數學中,三維球面(英文常寫作3-sphere)是球面在高維空間中的類比客體。它由四維歐幾里得空間中與一固定中心點等距離的所有點所組成。尋常的球面(或者說二維球面)是...
定義高斯球面映射(Gauss spherical map)古典曲面論的高斯映射的一種推廣.設二:M,,}R.}+n是n維光滑流形M"到歐氏空間的等距浸人,二也表示M"的位置向量.利用...
直道線是關於C-曲面的一個概念,是指C-曲面的直徑面截口。極限球面的“直道線”是指它的直徑面截口,即屬於已知極限球面的極限圓。球面的直徑面截口,即它的大圓...
霍普夫映射,即霍普夫纖維化。在拓撲學中,霍普夫纖維化(Hopf fibration,亦稱霍普夫纖維叢)是最早提出的纖維化,其中的纖維是圓圈,基空間是三維空間中的球面,而全空間...
