基本介紹
- 中文名:極大值
- 外文名:maximum
- 學科:數學
- 屬性:局部性概念
- 相關概念:極小值、極值、極值點
- 求法:一階導數、二階導數判別法等
定義
 圖1
圖1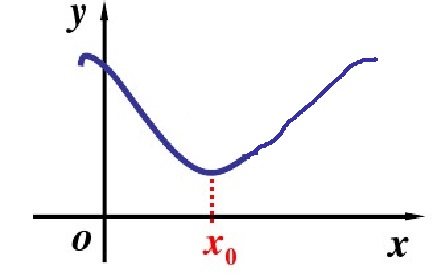 圖2
圖2數值區別
- 最大值是函式中最大的值,而極大值不是。
- 最大值一定高於函式中其他的值,極大值可以小於極小值。
- 最大值的值只有一個,而極大值的值可以有無限個。
- 最大值的定義區間為函式定義域,極大值可以自定義區間。

 圖1
圖1 圖2
圖2函式在某個極小區間內,存在自變數取值x,且存在比其大與比其小的自變數,這些自變數所對應的函式值均小於x對應的函式值。那么此函式值稱為極大值。即若對點x0的...
在數學分析中,函式的最大值和最小值(最大值和最小值)被統稱為極值(極數),是給定範圍內的函式的最大值和最小值(本地 或相對極值)或函式的整個定義域(全局...
極大值原理是對分析力學中古典變分法的推廣,能用於處理由於外力源的限制而使系統的輸入(即控制)作用有約束的問題。極大值原理是20世紀50年代中期蘇聯學者Л.С....
極值分布是指在機率論中極大值(或者極小值)的機率分布,從很多個彼此獨立的值中挑出來的各個極大值應當服從的機率密度分布數f(x)。...
若f(a)是函式f(x)的極大值或極小值,則a為函式f(x)的極值點,極大值點與極小值點統稱為極值點。極值點是函式圖像的某段子區間內上極大值或者極小值點的...
樣本極大值分布(distribution of the largest orderstatistic)樣本極大值的機率分布。設(X1,X2,…,Xo)是一個樣本容量為凡的樣本,則極大值x(o)=max(X1,…,...
求極大值與極小值的方法(Methodus ad disquirendam maximam et minimam),是17世紀西方的數學著作,由法國數學家費馬(Fermat,P.de)著,寫於1636年前。該文記述...
極大觀測值的機率分布。 ...... 極大觀測值的機率分布。 [1] 參考資料 1. 鄭家亨,統計大辭典,中國統計出版社,1995年03月第1版,第104頁 V百科往期回顧 詞...
模極大值的定義是滿足下列不等式的Wd2lX(n)的值記為MWd2lX(nkl)l=12.…Lkl=12.…Mlkl是極大值位。...
《最小國家的極大值》是2005年社會科學文獻出版社出版的圖書,作者是羅克全...... 《最小國家的極大值》是2005年社會科學文獻出版社出版的圖書,作者是羅克全....
第一極大值原理(first maximum principle)是描述位勢局部極大值蘊涵整體極大值的一個原理。...
強極大值原理(strong maximum principle) 二階橢圓方程的一個重要特性.在一定條件下,微分 方程在區域內部達到最大值的解只能是常數.設 在區域月(不必有界)中是...
X*的距離小於ε的X∈R(即X∈R且||X-X*||<ε)均滿足不等式f(x)≥f(x*),則稱X*為f(x)在R上的局部極小點(或相對極小點),f(x*)為局部極小值...
設minA和maxA分別為屬性A的最小值和最大值,將A的一個原始值v通過min-max標準化映射成在區間[new_minA, new_maxA]中的值v’。...
廣義極大值原理是第一極大值原理的推廣。α核都滿足廣義極大值原理。...... 廣義極大值原理是第一極大值原理的推廣。α核都滿足廣義極大值原理。...
在數學分析中,函式的最大值和最小值(最大值和最小值)被統稱為極值(極數),是給定範圍內的函式的最大值和最小值(本地 或相對極值),給定函式的整個定義域的...
極大值、極小值統稱為極值,使函式取得極值的點稱為極值點。...... 極大值、極小值統稱為極值,使函式取得極值的點稱為極值點。設n(n>2)元函式...
Minimax算法 又名極小化極大算法,是一種找出失敗的最大可能性中的最小值的算法(即最小化對手的最大得益)。通常以遞歸形式來實現。Minimax算法常用於棋類等由兩...
非極大值抑制(Non-Maximum Suppression,NMS),顧名思義就是抑制不是極大值的元素,可以理解為局部最大搜尋。這個局部代表的是一個鄰域,鄰域有兩個參數可變,一是...
極大似然估計方法(Maximum Likelihood Estimate,MLE)也稱為最大概似估計或最大似然估計,是求估計的另一種方法,最大概似是1821年首先由德國數學家高斯(C. F. ...
下鞅極大值不等式(maximalinequalityforsubmartingale)鞅論的一個重要不等式...... 下鞅極大值不等式(maximalinequalityforsubmartingale)鞅論的一個重要不等式 ...
積分的性質有:線性性、保號性、極大值極小值、絕對連續性、絕對值積分等。[1] 積分公式線性性 積分是線性的。如果一個函式f 可積,那么它乘以一個常數後仍然...
