定義,存在性,性質,
定義
高斯球面映射(Gauss spherical map)古典曲面論的高斯映射的一種推廣.設二:M,,}R.}+n是n維光滑流形M"到歐氏空間的等距浸人，二也表示M"的位置向量.利用歐氏平行性，把點二處的M”的一個單位法向量Y平移到R"十”的原點，它的像位於R..+”的單位超球面so+n-’上.這樣，就誘導了一個映射gY:U土M.,}So+p-，其中U土M'’表示M'’上的單位法叢.映射g，稱為M"的高斯球面映射.當n=2和p=1時，它就是經典的高斯映射.
存在性
對於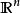
中的曲面
，定義映射
，其中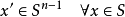
表示單位法向量。如果的第二基本形式正定，那么映射是單射，此時高斯映射(Gauss map)是良定的(well defined)。
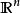
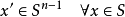
性質
高斯映射是局部微分同胚的。
