霍普夫映射

霍普夫映射，即霍普夫纖維化。在拓撲學中，霍普夫纖維化（Hopf fibration，亦稱霍普夫纖維叢）是最早提出的纖維化，其中的纖維是圓圈，基空間是三維空間中的球面，而全空間是四維空間中的超球面。

基本介紹

• 中文名：霍普夫映射
• 外文名：Hopf fibration
• 領域：數學
• 適用領域：拓撲學

簡介

在拓撲學中，霍普夫纖維化（Hopf fibration，亦稱霍普夫纖維叢）是最早提出的纖維化，其中的纖維是圓圈（1-球面，S¹），基空間是三維空間中的球面（2-球面，S²），而全空間是四維空間中的超球面（3-球面，S³）。容易驗證，它是非平凡的。即全空間S³與積空間S¹×S²不是拓撲同構的。

解釋

運用基本的拓撲學語言，霍普夫纖維化可以解釋為一個連續滿射（稱為投影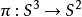） ，使得

（x在映射π下的原像，稱為纖維）與同胚；首先注意到，π是一個映射，這就意味著，任意兩個纖維是不交集，且所有的纖維的並等於全空間S，於是所有的纖維是S的一個劃分。通俗地說，霍普夫纖維化描述了用圓圈來填滿S的一種方式，其中每個圓圈對應S裡面的一個點。

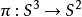
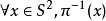
上面的條件還不足以使它成為一個纖維化，後者需要更強的條件，

，存在x的一個鄰域U(x)，使得與同胚；

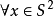
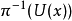
這個條件意味著，全空間S³與積空間S¹×S²在局部的拓撲性質上是不可區分的。如果全空間與積空間在整體的拓撲性質上也不可區分（即兩者同胚），則這個纖維化就是平凡的纖維化，例子如切叢。全空間與積空間的局部等價性又稱為局部平凡條件。霍普夫纖維化的重要性在於它是第一個非平凡纖維叢的例子，並且為纖維叢等數學概念的定義提供了模型基礎。

記號

上面描述的霍普夫纖維化可以記作：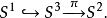

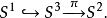
主叢

S³中的元素在四元數乘法下形成一個群G。給定一個纖維化之後，S³中對應於包含單位元的那個S¹纖維的元素自然地構成了G的一個子群H。考慮這個子群H中的元素對G中元素的右乘，它自然地構成了S³的一個自同構，這個自同構保持了纖維不變，即把纖維映射為纖維。

霍普夫纖維化給出了S³上的纖維用S²中的元素來進行參數化的一種方式。霍普夫纖維叢是一個主H-叢，意味著用H中的元素對S³進行變換後，我們仍然可以採用相同的參數化（即相同的映射π），唯一不同的，是每條纖維到S¹的同胚映射變為了另一個同胚映射。

拓展

上面提到的霍普夫纖維化是最早的霍普夫纖維化，有時也用這個詞來指代更廣泛的一類纖維叢。注意到前述纖維叢中涉及的三個超球面分別與複數域上的一些結構同胚（參見復射影直線）：

一個很自然的拓展是把上面的複數域換成實數或超複數，與實數、複數、四元數、八元數對應的霍普夫叢用上面的記號分別表為：

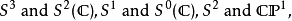
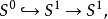
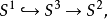
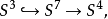
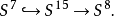
同倫論的研究表明，霍普夫叢只有上面四個，它們都不是平凡叢。

參見

• 海因茨·霍普夫
  
• 纖維叢