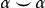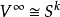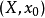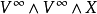基本介紹
- 中文名:霍普夫不變數
- 外文名:Hopf invariant
- 分類:同倫論
- 領域:數理科學
歷史,定義,性質,推廣到穩定映射,
歷史
1931年海因茨·霍普夫利用克利福德平行(Clifford parallel)構造了霍普夫映射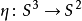 ,並通過利用圓周
,並通過利用圓周 對任意
對任意 的環繞數(=1),證明了
的環繞數(=1),證明了 是本質的,即不同倫於常值映射。隨後證明了同倫群
是本質的,即不同倫於常值映射。隨後證明了同倫群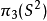 是由
是由 生成的無限循環群。1951年,讓-皮埃爾·塞爾證明了對一個奇數維球面(n 奇)有理同倫群
生成的無限循環群。1951年,讓-皮埃爾·塞爾證明了對一個奇數維球面(n 奇)有理同倫群 是零除非 i = 0 或 n。但對一個偶數維球面( n 偶),在
是零除非 i = 0 或 n。但對一個偶數維球面( n 偶),在 次處多出一個無限循環同倫。
次處多出一個無限循環同倫。
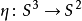



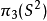



定義
設 是一個連續映射(假設
是一個連續映射(假設 )。則我們可以構造胞腔復形
)。則我們可以構造胞腔復形


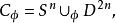





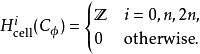




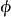
性質
對霍普夫映射霍普夫不變數是1(這裡 n=1,2,4,8,分別對應於實可除代數 ,而二重複疊
,而二重複疊 將球面上的一個方向送到它生成的子空間)。只有這些映射的霍普夫不變數是 1,這是最先由弗蘭克·亞當斯(Frank Adams)證明的一個定理,後來麥可·阿蒂亞利用 K-理論重新給出了證明。
將球面上的一個方向送到它生成的子空間)。只有這些映射的霍普夫不變數是 1,這是最先由弗蘭克·亞當斯(Frank Adams)證明的一個定理,後來麥可·阿蒂亞利用 K-理論重新給出了證明。


推廣到穩定映射
可以定義一種非常一般的霍普夫不變數概念,但需要一些同倫論知識預備:
現在令 是一個穩定映射,即在約化垂緯函子下穩定。F 的(穩定)幾何霍普夫不變數是
是一個穩定映射,即在約化垂緯函子下穩定。F 的(穩定)幾何霍普夫不變數是