球面,是在三維幾何空間內理想的對稱體。在數學上,這個項目是一個球體的表面或是邊界;但是在非數學的使用上,這是三維空間中一個球或是只是他的表面。在物理學中,球(通常被簡化與理想化)是能碰撞或堆積與占有空間的一個物體。
基本介紹
- 中文名:球面
- 外文名:sphere
- 單位球:r = 1是球的特例
- 球體:被球面緊貼包圍的立體
- 概念:單位球
相應概念
引用公式

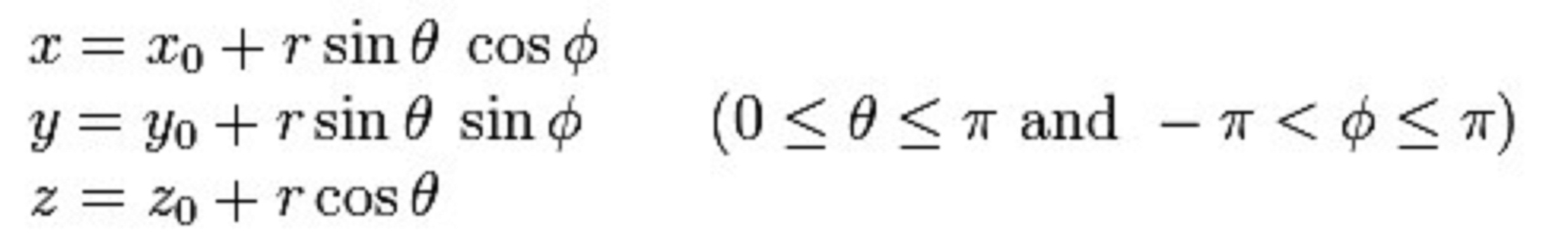


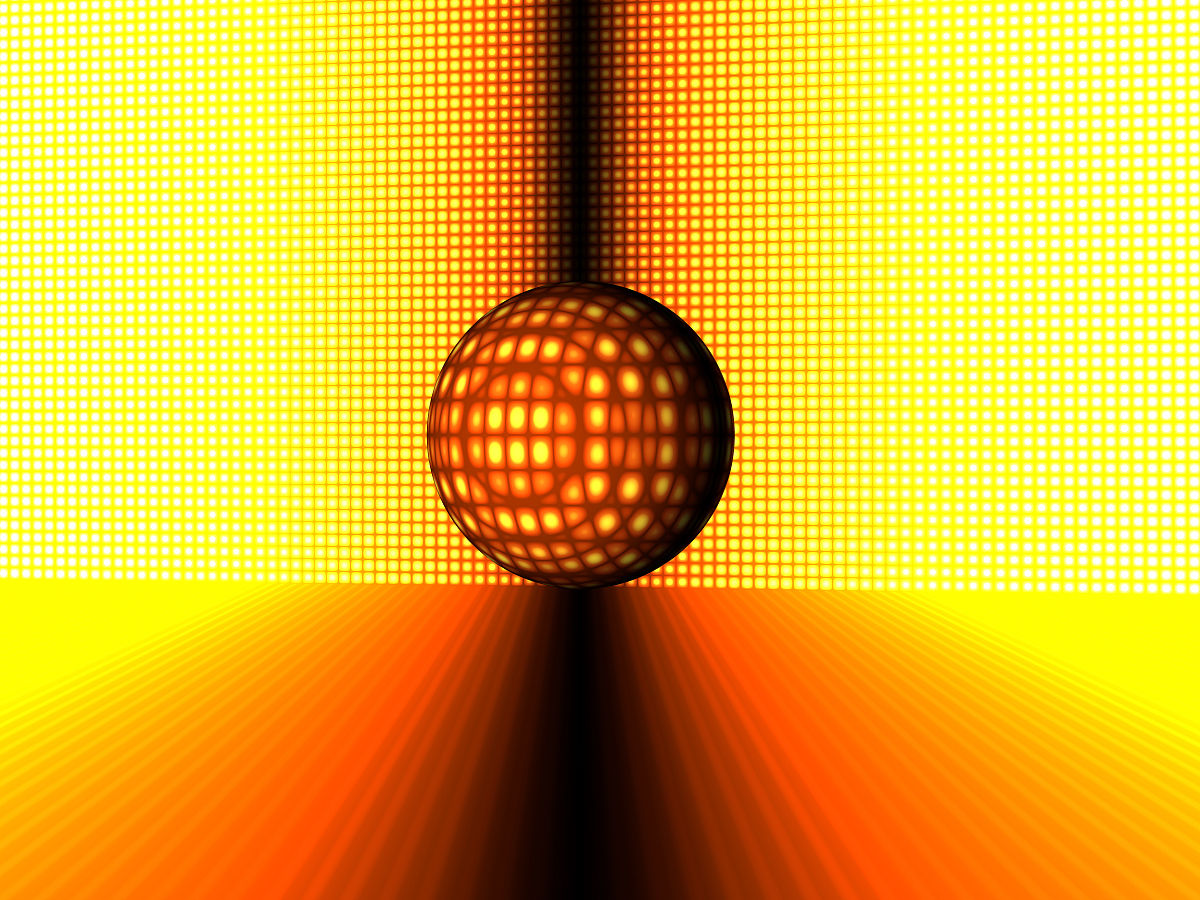
球面,是在三維幾何空間內理想的對稱體。在數學上,這個項目是一個球體的表面或是邊界;但是在非數學的使用上,這是三維空間中一個球或是只是他的表面。在物理學中,球(通常被簡化與理想化)是能碰撞或堆積與占有空間的一個物體。

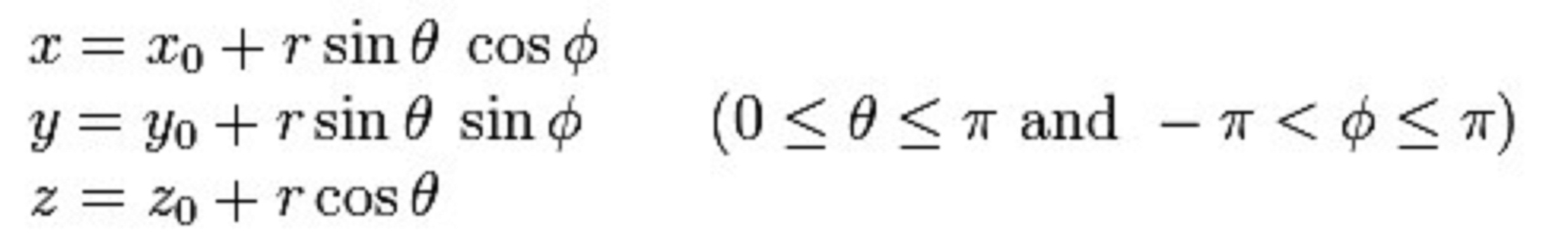


球面,是在三維幾何空間內理想的對稱體。在數學上,這個項目是一個球體的表面或是邊界;但是在非數學的使用上,這是三維空間中一個球或是只是他的表面。在物理學中...
反射面為球面的一部分的鏡面叫做球面鏡。球面鏡分為凸面鏡和凹面鏡兩類。用球面的內側作反射面的球面鏡叫做凹面鏡,用球面的外側作反射面的球面鏡叫做凸面鏡。...
球面三角是研究球面三角形的邊、角關係的一門學科。從十六世紀起由於天文學、航海學、測量學等方面的發展,球面三角逐漸形成了獨立學科。從平面三角學我們知道,一...
球面度(Sr=Steradian)是立體角的計量單位。面積為半徑平方(r2)的球表面對球心的張角等於1球面度。因為球的表面積是4πr2,所以,整個球面有4π球面度。一個發光...
所謂球面和非球面,主要是針對鏡頭(各種相機、顯微鏡等鏡頭)、眼鏡(包括隱形眼鏡)的鏡片幾何形狀而言,即球面鏡片與非球面鏡片。二者在幾何形狀上的差別決定了它們在...
複平面加上點後稱為擴充複平面(extended complex plane),與它對應的就是整個球面,稱為復球面(complex sphere)。簡單說來,擴充複平面的一個幾何模型就是復球面。...
球面圖形(spherical figure)是球面幾何的研究對象,指所有點都在同一球面上的幾何圖形,在球面幾何學中,主要研究的球面圖形有球面大圓、小圓、球面多邊形、球面二角形...
非球面鏡片它的表面弧度與普通球面鏡片不同,為了追求鏡片薄度就需要改變鏡片的曲面,以往採用球面設計,使得像差和變形增大,結果出現明顯的影像不清,視界歪曲、視野...
黎曼球面由19世紀數學家黎曼而得名。也稱為復射影直線,記為 ,和 擴充複平面,記為 或者. 從純代數的角度,複數加上一個無窮遠點構成一個數系稱為擴充複數。...
球面圓(spherical circle)是球面幾何的基本概念之一,指球面在空間中與平面相交時的交線圓,包括平面通過球心時交成的球面大圓和平面不通過球心時與球面相交而成的...
量子力學中,以自旋物理與核磁共振專家費利克斯·布洛赫(Felix Bloch)姓氏命名的布洛赫球面是一種對於雙態系統中純態空間的幾何表示法。在討論量子位元的場合上常常...
球面三角學是球面幾何學的一部分,主要在處理、發現和解釋多邊形 (特別是三角形) 在球面上的角與邊的聯繫和關聯。在天文學上的重要性是用於計算天體軌道和地球表面...
球面折射的規律是多數光學鏡頭設計中的基本規律,因為許多複雜的光學鏡頭,都由一系列球面組成的。...
球面電影編輯 鎖定 美國宇航局上映在球體上播放的電影 [1] [導讀]據國外媒體報導,電影《Water Falls》是科學與藝術的結合物,但它的觀影形式非常特別。 [1] ...
500米口徑球面射電望遠鏡(Five-hundred-meter Aperture Spherical Telescope),簡稱FAST,位於貴州省黔南布依族苗族自治州平塘縣克度鎮大窩凼的喀斯特窪坑中,工程為國家...
球面投影 ...... 球面投影圖集 球面投影圖冊 V百科往期回顧 詞條統計 瀏覽次數:次 編輯次數:2次歷史版本 最近更新: 創建者:百科ROBOT...
球面波是指波陣面為同心球面的波。球面波在自由場的傳播過程中,其聲場中聲壓幅度與到聲源中心的距離成反比例地衰減變化。當聲源的尺度遠小於媒質中的聲波波長(...
球面上兩點之間的最短連線的長度,就是經過這兩點的大圓在這兩點間的一段劣弧的長度。(大圓就是經過球心的平面截球面所得的圓)
外球面球軸承實際上是深溝球軸承的一種變型,特點是它的外圈外徑表面為球面,可以配入軸承座相應的凹球面內起到調心的作用。外球面軸承主要用來承受以徑向負荷為主...
球是以半圓的直徑所在直線為旋轉軸,半圓面旋轉一周形成的旋轉體,也叫做球體(solid sphere)。球的表面是一個曲面,這個曲面就叫做球面,球的中心叫做球心。
一個半圓繞直徑所在直線旋轉一周所成的空間幾何體叫做球體,簡稱球,半圓的半徑即是球的半徑。球體是有且只有一個連續曲面的立體圖形,這個連續曲面叫球面。球體在...
以觀測點為球心,構造一個單位球面;任意物體投影到該單位球面上的投影面積,即為該物體相對於該觀測點的立體角。因此,立體角是單位球面上的一塊面積,這和“平面角...
球體表面積是指球面所圍成的幾何體的面積,它包括球面和球面所圍成的空間,球體表面積的計算公式為S=4πr²=πD²,該公式可以利用求體積求導來計算。...
