基本介紹
- 中文名:八維空間
- 外文名:eight-dimensional space
- 提出者:巴克哈德 海姆
- 提出時間:1957年
- 套用學科:物理學,幾何學
- 適用領域範圍:物理學
定義
提出
內容
幾何學中
八維多胞形
七維球面
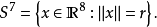

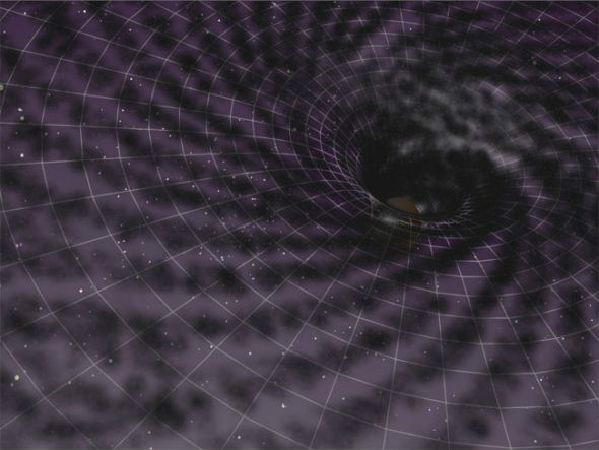

八維空間(eight-dimensionalspace)是物理學界的一個理論,這一理論認為八維空間分為X維(物體的長)、Y維(物體的寬)、Z維(物體的高)、時間維、速度維、溫度維...
空間維,為數學、物理術語。“維”是一種度量,在三維空間坐標上,加上時間,時空互相聯繫,就構成四維時空。四維是動態空間(因為有了時間)。...
八維,更為複雜。現在物理學界公認的理論是八維空間,分為X維(物體的長)、Y維(物體的寬)、Z維(物體的高)、時間維、重力維、電磁力維、萬有引力維、萬有...
他的團隊是香港騎士團隊,現在他們遇到了一個非常重要的任務,即要阻止罪惡的生物從第八維空間進入我們的空間。類型 愛情/科幻/冒險/喜劇 導演 W.D. Richter ...
八維空間音樂文化藝術工作室 電影海報 原創背景音樂編配 譚宏超 王進峰片尾曲原創《飄》詞/曲/編/配器/唱/ 譚宏超飄(就這樣)隨風飄 在這座陌生城市...
八維空間亦真亦幻;殘廢之海到處充滿著兇險……燉肉蟲不管是動物還是人反正是肉就想燉;大醜一哭就發洪水;小丑一笑就出怪事,幽默、駭人的故事層出不窮,人物的...
真·萬化跳出七維空間,進入八維空間不僅能看到無數個平行宇宙,而且能自由穿梭於每個平行宇宙之間。 真·歸一跳出八維,進入九維空間,宇宙也不是宇宙,只是一條線無...
超禁忌動漫八維空間 超禁忌動漫九維空間 超禁忌動漫十維空間 超禁忌動漫十一維空間 星矢、冰河、一輝被毀滅神幹掉後,被魔魅復活並控制,能力最終給了張志強。...
只含有一個未知數(一元),並且未知數項的最高次數是八次的整式方程叫做一元八...一元八次方程求解 適用領域範圍 八維空間有關問題 英文名 Formula for Octic...
幸運的是我得到八維空間,“什麼,不做貢獻就死亡。”路過的請注意這裡:這是一篇懶人的建國史這是一篇女變男不娘的文這是一篇主角渴望平凡,又遇到各種狀況不得不...
八維空間音樂文化藝術工作室 劇照 原創背景音樂編配 譚宏超 王進峰 皮鞋的故事片尾曲 原創《飄》 詞/曲/編/配器/唱/ 譚宏超 劇照 飄(就這樣)隨風飄 ...
