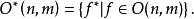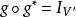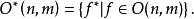正交內射

一切正交內射之集為O(n,m)，則當m=n時，O(n,n)=O(n)便是正交群。

基本介紹

• 中文名：正交內射
• 外文名：orthogonal ingjection
• 適用範圍：數理科學

簡介

若

且對 有

則稱f為一個正交內射。

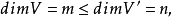
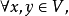
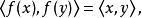
記一切正交內射之集為O(n,m)，則當m=n時，O(n,n)=O(n)便是正交群。

性質

設V,V'為內積空間，對線性映射f:V→V'，令f*:V'→V對於一切x∈V,y∈V'，滿足內積的關係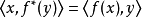

則由f惟一確定的線性映射f*稱為f的共軛。

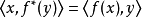
判定

f 是正交內射，若且唯若f*°f=I_v。

當f是正交內射時，f*稱為正交投影，因此線性映射g:V'→V為正交投影，若且唯若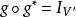 記一切從內積空間Rⁿ到R^m的正交投影之集為