正交系是互相正交的函式系的簡稱,用於微分方程、積分方程、計算方法等數學領域。
基本介紹
- 中文名:正交系
- 外文名:orthogonal set
- 概念:互相正交的函式系
- 別稱:正交函式系
- 套用:微分方程、積分方程、計算方法等
定義
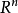
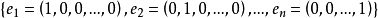
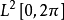
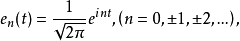
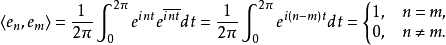
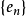
相關定理
定理1
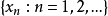
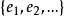
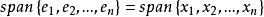
定理2
定理3
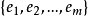
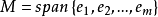
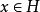
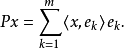
定理4
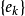
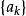
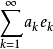
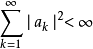

定理5

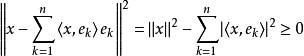
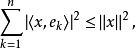
定理6
定理7



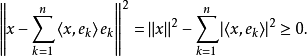
定理8
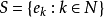
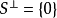
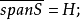
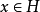

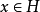
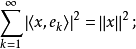
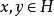
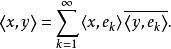
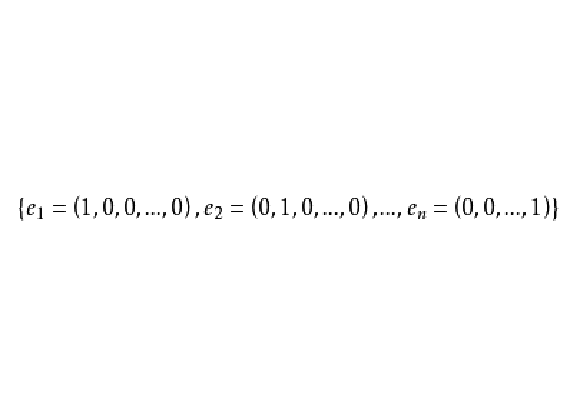
正交系是互相正交的函式系的簡稱,用於微分方程、積分方程、計算方法等數學領域。
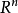
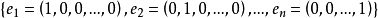
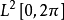
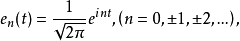
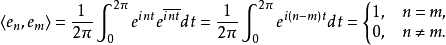
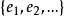
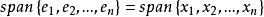
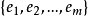
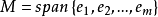
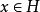
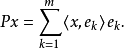
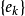
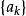
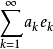
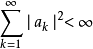


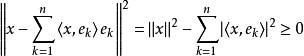
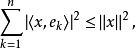



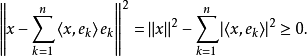
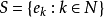
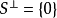
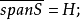
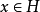

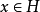
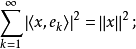
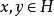
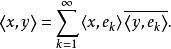
正交系是互相正交的函式系的簡稱,用於微分方程、積分方程、計算方法等數學領域。...... 正交系是互相正交的函式系的簡稱,用於微分方程、積分方程、計算方法等數學領域...
設M是內積空間X的一個不含零子集,若M中向量兩兩正交,則稱M為X中的正交系,又若M中向量的範數都為1,則稱M為X中的規範正交系。...
沃爾什正交系是拉德瑪赫爾函式系的完備化,是由美國數學家沃爾什於1923年建立的。...... 沃爾什正交系是拉德瑪赫爾函式系的完備化,是由美國數學家沃爾什於1923年建立...
正交化是指將線性無關向量系轉化為正交系的過程。設{xn}是內積空間H中有限個或可列個線性無關的向量,則必定有H中的規範正交系{en}使得對每個正整數n(當{xn...
弱F是H中的完全正交系,如果對每個x∈H,F使帕塞瓦爾等式成立,就稱F是完備正交系。...... 弱F是H中的完全正交系,如果對每個x∈H,F使帕塞瓦爾等式成立,就稱F...
正交V系統是宋瑞霞教授2005年在齊東旭教授U系統基礎上創作的完備正交系統。 下面是V系統的簡單介紹: 從[0,1]區間上函式生成元出發,構造了一類的正交完備函式系,...
把線性無關向量系進行正交化的過程,稱為格拉姆-施密特正交化過程。...... 設M是內積空間X的一個不含零子集,若M中向量兩兩正交,則稱M為X中的正交系,又若M中...
正交是線性代數的概念,是垂直這一直觀概念的推廣。作為一個形容詞,只有在一個確定的內積空間中才有意義。若內積空間中兩向量的內積為0,則稱它們是正交的。如果...
正交多項式系(system of orthogonal polynomials)是正交函式系的一種。...... 正交多項式系(system of orthogonal polynomials)是正交函式系的一種。中文名 正交多項式...
曲面上使兩族參數曲線彼此正交的參數系稱為曲面的正交坐標系。正交坐標系的特徵是其第一基本型的係數F≡0,因此它的第一基型成為I=Edu²+Gdv²。在曲面上...
拉德馬赫函式系是有重要力量和套用價值的一個特殊正交函式系。拉德馬赫函式系的函式在二進區間上取值1,-1或0,它與在套用中有重要意義的沃爾什函式系關係密切。...
沃爾什正交系是從二進位表示出發的。對於任何正整數p>2,亦可從p進位出發,建立新的沃爾什正交系。只是此時對於函式的諸如連續、可微以及李普希茨條件等的定義都應...
設{ek}是內積空間H中一族彼此不同的向量,如果其中任何兩個向量都正交,即當k≠j時,(ek,ej)=0,則稱{ek}是一正交系;如果其中每個向量的範數又都是1,即對...
4.9.3正交系中張量表達式的物理分量形式179習題180第5章曲面上的張量分析1845.1曲面的基本知識1845.1.1曲面的參數方程與Gauss坐標1845.1.2曲面的基本矢量185...
藉助於沃爾什函式系的逼近稱為沃爾什逼近。沃爾什逼近是沃爾什正交系中函式線性組合的逼近。...
司捷克洛夫定理是關於L2[a,b]中規範正交系為完備系的一個定理。...... 司捷克洛夫定理是關於L2[a,b]中規範正交系為完備系的一個定理。設{wk(x)}是L2[a,...
都是正數,折射率也是正數,現在我們可以稱它為“右手征材料”)中,由電磁場的麥克斯韋方程知道,入射電磁波的電場、磁場和波矢(相位傳播方向)三者構成右手正交系。...
