沃爾什正交系

沃爾什正交系是拉德瑪赫爾函式系的完備化，是由美國數學家沃爾什於1923年建立的。

基本介紹

• 中文名：沃爾什正交系
• 外文名：Walsh orthogonal system
• 適用範圍：數理科學

簡介

沃爾什正交系是拉德瑪赫爾函式系的完備化。

記為拉德馬赫爾正交系，即

定義 對於正整數 n，若其二進位表示是，這裡 是整數，則定義

稱 為沃爾什函式，而稱 為沃爾什正交系。

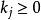
性質

沃爾什正交系是由美國數學家沃爾什於1923年建立的，它不僅在 [0,1] 上是規範的正交集，而且在 中是完備的。

此外，對於任何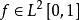，如果對 k=0,1,...,都有

則 f(x) 在 [0,1] 上幾乎處處等於零。

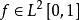
沃爾什正交系與哈爾正交系 有如下的關係：

一般的關係是由歸納法給出的，如果記

其實，則

其實矩陣是用如下方法得到的：依次將的每一行重複寫成兩行，得到一個 2^n-1 列2ⁿ行的矩陣，它恰好是的左半個，然後將它向右延伸2^n-1列，延伸的奇數行就是左半矩陣的奇數行，延伸的偶數行就是左半矩陣的偶數行的相反符號，例如

則

人們又稱上述定義的沃爾什正交係為按自然序排列的：

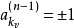
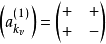
推廣

在工程上為了套用方便，還有一種列率序排列的，對集{0,1}引入偽加運算（如圖所示）：

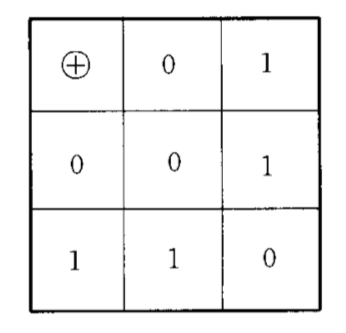圖1

0⊕0=0，

0⊕1=1，

1⊕0=1，

1⊕1=0。

一個正整數 n 的二進位表示是：

則稱 為n 的格雷代碼，相應的二進位表示的數是

定義，並稱為列率序的沃爾什正交系，自然也是 中的規範且完備的正交系，而且它與三角函式系有著更相似的性質。例如有，這裡 k⊕j 的含義是設 k 和 j 有二進位表示

則