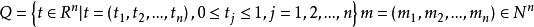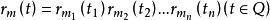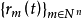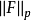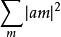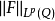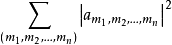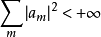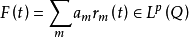拉德馬赫函式系

拉德馬赫函式系是有重要力量和套用價值的一個特殊正交函式系。拉德馬赫函式系的函式在二進區間上取值1，-1或0，它與在套用中有重要意義的沃爾什函式系關係密切。

基本介紹

• 中文名：拉德馬赫函式系
• 外文名：system of Rademacher functions
• 適用範圍：數理科學

簡介

拉德馬赫函式系是有重要力量和套用價值的一個特殊正交函式系。

在一維情形，可先定義函式

然後將 按周期 1 做延拓，即令 （[t]為 t 的整數部分）或 ，再定義

則 稱為區間 [0,1]上的拉德馬赫函式系，它是[0,1]上的正交系，但不是完備的。

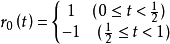
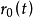
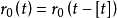
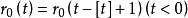
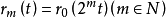
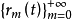
性質

拉德馬赫函式系有如下重要性質：

設數列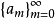 有

則級數

在[0,1]上幾乎處處收斂，其和 對一切 成立；還存在正的常數 A_p和B_p，使

因此

可用以刻畫。

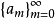
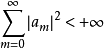
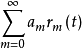
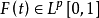
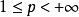
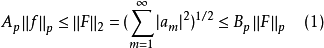
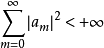
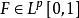
套用

拉德馬赫函式系的函式在二進區間上取值1，-1或0，它與在套用中有重要意義的沃爾什函式系關係密切，在套用中常稱為開關函式，是由德國數學家拉德馬赫於1922年提出的，還有一些等價的定義方式（例如可表示成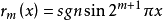，這裡sgn表示符合函式）。

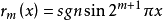
推廣

拉德馬赫函式系可以推廣到高維空間，記

則由定義的函式系 可稱為 Q 上的拉德馬赫函式系，它具有與一維情形相同的性質的重要意義，特別地，若將和分別理解成和

則由仍有

並且(1)式（其中各有關量均按n維情形定義）仍然成立。