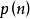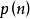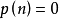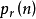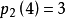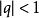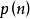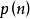分拆是指將一個正整數表示成不大於其自身的一個或幾個正整數的無序和，分拆數（partition number）則指不同的分拆方式的數目。分拆數源於分拆函式（partition function）。分拆函式也是表示兩個事物之間的對應關係：輸入給定的x便有對應的f(x) 輸出。
基本介紹
- 中文名：分拆函式
- 外文名：partition function
簡介,實例,發展,
簡介
命 n 為一個正整數。把 n 分成若干個不計次序的整數之和的一種方法稱為 n 的一種分拆。例如 4=3+1=2+2=2+1+1=1+1+1+1，所以 4 點不同分拆有 5 種。命 n 的不同分拆方法為
，則稱為分拆函式（partition function）。常約定
，實際上，這是一種無限制的分拆。還可以對被加數加以限制。例如限定被加數不超過 r 。這種分拆函式記作
。有
。當
時，稱冪級數
為分拆函式的母函式或生成函式（generating function）。
用初等數論的方法可以得出估計式
。略用一點初等分析，即可的出估計式
。再由陶伯型定理或複變函數論可得出的漸近式。最後，由模函式理論的這結果及解析數論方法，拉德馬赫（H.Rademacher）得到了的展開式。這裡是一個例子，以表明各種方法的深度。
實例
分拆函式p（n）的值為：對於給定整數n，其拆分方式種類。例如：4的分拆方式有：1+1+1+1，1+1+2，1+3，2+2和4，所以p（4）=5。
n | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
p（n） | 1 | 1 | 2 | 3 | 5 | 7 | 11 | 15 | 22 | 30 | 42 | 56 | 77 | 101 |
發展
分拆函式及其對應的分拆數可能看起來很直觀，但幾個世紀以來，理論學家們一直努力尋找這些數值的關聯模式，以便預知、計算分拆數。或者建立分拆數與其他函式、定理之間的關係。但均以失敗告終。
印度數學家拉瑪努金（Srinivasa Ramanujan）通過研究發現，從p（4）開始，每第5個數值均可被5整除，他還證明了從p（5）開始每第7個拆分數可被7 整除，從p（6）開始，每第11個數可被11整除。該猜想即“拉瑪努金同餘式”。
由於拉瑪努金沒有記錄自己的證明過程，後世無法知曉公式成立的原因及意義。
埃默里大學數論教授肯恩·小野（Ken Ono ）進一步研究發現，如果將分拆函式看作經過變形的模形式，就可以證明拉瑪努金是對的。小野回憶“如果這個宇宙的星星是分拆數，有了它之後，當你再觀測宇宙，你能看到宇宙中存在非常多的星系（即同餘式）。”於是小野證明分拆同餘式有無窮多個。
通過運算元等理論工具，小野等人構造出了能夠快速準確計算巨大分拆數的公式。
