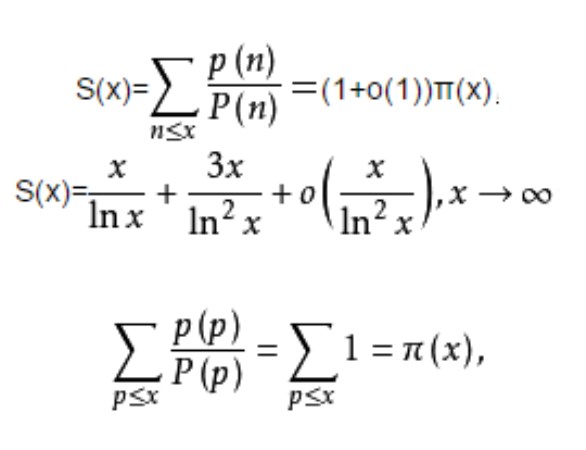廣義素數定理(generalized prime number theorem)是素數定理的推廣，廣義素數定理是1982年愛爾特希(P.Erdös)提出和證明的。素數定理指素數出現的規律，可分為自然數素數定理、函式素數定理及廣義素數定理等，“自然數素數定理”和“函式素數定理”可統稱為狹義素數定理。
基本介紹
- 中文名：廣義素數定理
- 外文名：generalized prime number theorem
- 所屬學科：數學
- 所屬問題：初等數論(素數分布)
- 提出者：愛爾特希(P.Erdös)
基本介紹,相關介紹,愛爾特希,
基本介紹
設整數n>1，P(n)表n的最大素因子，p(n)表n的最小素因子，則有
S(x)=
=(1+o(1))π(x)；(1)
S(x)=
； (2)
當n僅取素數時，
所以，S(x)是π(x)的一種推廣。而(1)表明S(x)與π(x)是等價的，(3)式則進一步求出了S(x)的漸近公式，但注意到對任意正整數A，由於有
相關介紹
定義1 素數定理指素數出現的規律，可分為自然數素數定理、函式素數定理及廣義素數定理等，每種素數定理，又分為實際素數定理和理論素數定理等，這裡說的規律包括某範圍的機率分布函式、素數個數、均方差及邊界等量的集合，它將目前說的“素數定理”的概念進行了擴展，其中，自然數素數定理是函式素數定理的特例，函式素數定理是自然數素數定理的推廣，故“自然數素數定理”和“函式素數定理”可統稱為狹義素數定理。
定義2 在t≤N內的函式或條件H(t)中，出現狹義或廣義素數的規律，定義為狹義或廣義素數定理，H(t)的素數率記為
，素數個數實際值及理論值分別表為π(H(N))及Π(H(N))，則
π(N,x)=π(N)ρ(N,x)
Π(N,x)=Π(N)P(N,x)
愛爾特希
愛爾特希(P.Erdös)是匈牙利數學家。猶太人。生於布達佩斯，是兩位中學數學教師的獨子，一個數學神童，3歲時已能心算三位數的乘法，4歲時便發現了負數。1930年進入布達佩斯大學學習數學，1934年畢業並獲得博士學位。1934年10月，赴英國曼徹斯特，從事為期4年的博士後研究。之後不間斷地旅行了50多年，從未在一個地方停留一個月以上，沒有妻小，沒有職業，沒有其他嗜好，完全獻身於對美妙的數學問題和新奇的數學技巧的追求之中，以近乎瘋狂的節奏，奔波於四大洲一個又一個大學或研究中心。他是匈牙利科學院院士，荷蘭皇家研究院院士，以及倫敦數學會、美國數學會會員。
愛爾特希的數學興趣包括數論、集合論、組合數學、圖論、機率論及其套用以及數理邏輯等。尤其在數論方面的工作最為突出，被譽為“一心迷戀於數的學者”。在整數分析問題的研究中，17歲時他便給出了“在任何一個(大於1的)整數和它的兩倍數之間必定存在素數”的一個簡單證明，轟動了匈牙利數學界。1942年，他用初等的函式論方法估計了n的分拆數p(n)的值。還提出了一個猜想：如果n個等差數列沒有覆蓋住自然數列，那么必存在0<m<2n，m不屬於上述任何一個等差數列。1940年，他證明了存在無窮多個自然數n，使得Pn+1-Pn<clgPn，其中Pn為第n個素數，c為歐拉常數。1949年，他取得了他數學研究上的最大成功，即他與賽爾伯格(A.Selberg)合作對“描述素數統計分布的公式”給出了一個“初等”證明，震撼了數學界。他還研究過親和數的分布問題。在組合數學中，他對其中引人注目的拉姆齊理論作出過開拓性的工作。
愛爾特希是位超級解題能手，一位數學苦行僧，他還善於與各國數學家合作研究，與他合作過的人超過了250人，比歷史上任何一位數學家的合作者都多。
愛爾特希是世界上最著名、最富有廣泛旅行經歷、最多產的數學家，現已發表1 000多篇數學論文，而且每篇論文至少包含一個值得注意的新結果。他還寫有300多種論著，主要著作有《數論的一些新進展和當前的問題》(1965)、《組合分析中的機率方法》等。他不但在匈牙利和以色列為學生設立了兩個獎學金，還為證明一些有趣的問題設定了10美元至3 000美元的現金獎，以促進數學的發展。由於對數學的傑出貢獻，他榮獲1983—1984年度的沃爾夫獎。
