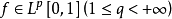沃爾什逼近

藉助於沃爾什函式系的逼近稱為沃爾什逼近。沃爾什逼近是沃爾什正交系中函式線性組合的逼近。

基本介紹

• 中文名：沃爾什逼近
• 外文名：Walsh approximation
• 表達式：w0(x)=1
• 適用領域範圍：數學
• 適用領域範圍：數學，工程

簡介

沃爾什逼近是沃爾什正交系中函式線性組合的逼近。

沃爾什多項式

設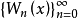 是沃爾什正交系，對於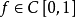或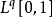，人們首先考慮展開f(x)為沃爾什-傅立葉級數

的收斂性，以及此級數的部分和

對f(x)在C[0,1] 度量或度量下的逼近性態，其次是對於任意給定的數（實的或復的），稱

為 n 階沃爾什多項式，記其全體為 T_n。

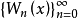
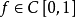
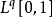
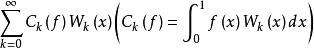
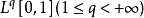
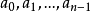
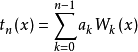
定義

設

考慮用T_n 中的的度量下逼近 f 常記

這裡

易知當n→∞時，E_n(f)單調減少收斂於零。

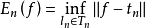
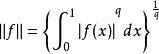
套用

與三角多項式逼近相似，在沃爾什逼近中，人們關心的亦是n階沃爾什多項式對函式f的最佳逼近E_n(f)收斂於零的速度與函式f(x)的構造性之間的關係，諸如三角多項式逼近的正定理與逆定理等，也已為人們所建立。

20世紀80年代以來，這方面的研究頗受人們重視。

推廣

沃爾什正交系是從二進位表示出發的。對於任何正整數p>2，亦可從p進位出發，建立新的沃爾什正交系。只是此時對於函式的諸如連續、可微以及李普希茨條件等的定義都應適當改變。此外，也已有人研究多元的沃爾什函式系。

這些理論在資訊理論、線性系統、通訊等方面已有或將有廣泛的套用。特別對於逐段光滑的函式，沃爾什正交系有時會出現較三角函式系更有效的性能。