基本介紹
- 中文名:數量積
- 外文名:dot product; scalar product
- 別名:標量積、點積、內積、向量的積
- 運算類型:二元運算
- 點積的三個值:u、v、u,v夾角的餘弦
- 點積的值:u,v的點積=|u||v|cos<u,v>
- 套用學科:線性代數
定義
廣義定義
代數定義




幾何定義






定義的等價性











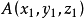
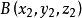



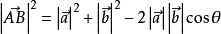


點積的值
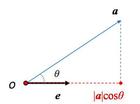 點積
點積運算律



套用

內積一般指本詞條





















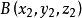



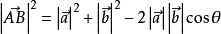


 點積
點積




在數學裡面,內積空間是增添了一個額外的結構的向量空間。這個額外的結構叫做內積,或標量積,或點積。這個增添的結構允許我們談論向量的角度和長度。內積空間由歐幾里得...
函式的內積用於描述兩個函式之間的關係。它在傅立葉級數中起到了奠基性的作用,在其他方面也有用途。...
內積羅瓦克是一名足球運動員,球場位置是前鋒,效力於蘭斯科羅納俱樂部。...... 內積羅瓦克是一名足球運動員,球場位置是前鋒,效力於蘭斯科羅納俱樂部。中文名: 內積羅瓦克...
在數學中,數量積(dot product; scalar product,也稱為點積)是接受在實數R上的兩個向量並返回一個實數值標量的二元運算。它是歐幾里得空間的標準內積。兩個向量a...
在數學中,希爾伯特空間是歐幾里德空間的一個推廣,其不再局限於有限維的情形。與歐幾里德空間相仿,希爾伯特空間也是一個內積空間,其上有距離和角的概念(及由此引申...
數學上,克羅內克積是兩個任意大小的矩陣間的運算。克羅內克積是張量積的特殊形式,以德國數學家利奧波德·克羅內克命名。中文名 克羅內克積 外文名 Kronecker product...
名稱標積/內積/數量積/點積矢積/外積/向量積/叉積 運算式(a,b和c粗體字,表示向量) a·b=|a||b|·cosθ a×b=c,其中|c|=|a||b|·sinθ,c的方...
度量矩陣是指歐氏空間的一組基之間的內積作為元素構成的矩陣。度量矩陣具有下列性質:複數域上度量矩陣是赫米特矩陣(是指和其共軛轉置相等的矩陣. 設矩陣A∈Cnxn, ...
是兩個希爾伯特空間,分別帶有內積 和 。構造H1和H2的張量積 如下:考慮他們的作為線性空間的張量積 。 和 上的內積自然地擴展到H上:由...
正交是線性代數的概念,是垂直這一直觀概念的推廣。作為一個形容詞,只有在一個確定的內積空間中才有意義。若內積空間中兩向量的內積為0,則稱它們是正交的。如果...
外積一般指兩個向量的向量積;或在幾何代數中,指有類似勢的運算如楔積。這些運算的勢是笛卡爾積的勢。這個名字與內積相對,它是有相反次序的積。這裡寫的是外積,...
柯西—施瓦茨不等式的一個重要結果,是內積為連續函式。 [2] 柯西—施瓦茨不等式證明3 柯西—施瓦茨不等式有另一形式,可以用范的寫法表示:...
時,這個範數一定可以誘導內積;完備的內積空間稱為希爾伯特空間。(4) 如果去掉範數定義中的正定性,那么得到的泛函稱為半範數(seminorm或者叫準範數),相應的線性空間...
這些數學空間可以被擴展來套用於任何有限維度,而這種空間叫做 n 維歐幾里得空間(甚至簡稱 n維空間)或有限維實內積空間。這些數學空間還可被擴展到任意維...
(4)給定任何左矢<Φ|及右矢|Ψ>,內積的一個公理性質指出:狄拉克符號量子力學 編輯 量子力學是研究微觀粒子運動規律的理論,是現代物理學的理論基礎之一。量子力學...
支持向量機通過某非線性變換 φ( x) ,將輸入空間映射到高維特徵空間。特徵空間的維數可能非常高。如果支持向量機的求解只用到內積運算,而在低維輸入空間又存在某...
在泛函分析中,卷積、旋積或摺積(英語:Convolution)是通過兩個函式f和g 生成第三個函式的一種數學運算元,表征函式f與g經過翻轉和平移的重疊部分的面積。 如果將...
