在量子力學中,所有的物理規律在一個希爾伯特空間中表示,而這個希爾伯特空間可以稱為右矢量空間。在這個空間中可以選取一組線性獨立且完備的基矢量,稱為基右矢。在定義了內積之後,我們可以對這組基右矢進行更嚴格的要求——正交;事實上通過施密特正交化(Schmidt orthogonalization),我們也總能將一組線性獨立的基矢變成正交的。這樣得到的一組完備且正交的右矢量,我們稱之為正交右矢。
基本介紹
- 中文名:正交右矢
- 外文名:orthogonal base kets
引入,性質,
引入
基於右矢量空間引入正交右矢:
首先在右矢量空間中定義雙線性運算,我們稱之為內積:
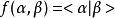
其滿足雙線性:


此外我們要求:
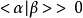

性質
一組正交右矢 可以完備地表示右矢量空間的任一右矢量:
可以完備地表示右矢量空間的任一右矢量:


然後其滿足正交歸一條件:

