因子載荷 aij 的統計意義就是第i個變數與第 j 個公共因子的相關係數即表示 Xi 依賴 Fj 的份量(比重)。統計學術語稱作權,心理學家將它叫做載荷,即表示第 i 個變數在第 j 個公共因子上的負荷,它反映了第 i 個變數在第 j 個公共因子上的相對重要性。
基本介紹
- 中文名:因子載荷
- 外文名:factor loading
- 別名:權
- 範疇:統計學
- 英文:factor loadings
簡介
因子分析
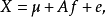

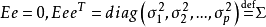




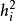

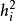
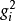

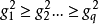

因子載荷 aij 的統計意義就是第i個變數與第 j 個公共因子的相關係數即表示 Xi 依賴 Fj 的份量(比重)。統計學術語稱作權,心理學家將它叫做載荷,即表示第 i 個變數在第 j 個公共因子上的負荷,它反映了第 i 個變數在第 j 個公共因子上的相對重要性。
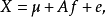

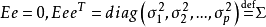




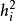

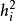
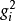

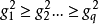
因子載荷 aij 的統計意義就是第i個變數與第 j 個公共因子的相關係數即表示 Xi 依賴 Fj 的份量(比重)。統計學術語稱作權,心理學家將它叫做載荷,即表示第 i ...
因子分析的基本目的就是用少數幾個因子去描述許多指標或因素之間的聯繫,即將相關比較密切的幾個變數歸在同一類中,每一類變數就成為一個因子,以較少的幾個因子反映...
為使因子分析法求出因子載荷陣結構簡化,便於對主因子進行專業上解釋,常對因子載荷陣施行變換或稱因子旋轉。最常用的方法是方差最大的正交旋轉法,使旋轉後的因子...
因子分析是指研究從變數群中提取共性因子的統計技術。最早由英國心理學家C.E.斯皮爾曼提出。他發現學生的各科成績之間存在著一定的相關性,一科成績好的學生,往往...
因子分析的數學模型是將變數 (或樣品)表示為主因子的線性組合,但有時也需要反過來將主因子表示為原始變數的線性組合,即Fi=βi1x1+βi2x2+…+βipxp,i=1,2...
探索性因子分析法(Exploratory Factor Analysis,EFA)是一項用來找出多元觀測變數的本質結構、並進行處理降維的技術。因而,EFA能夠將具有錯綜複雜關係的變數綜合為少數幾...
4、ai6叫因子負荷(或載荷、權數),表示第i個上市公司在六個因子方面的能力,ui是第I個上市公司的能力不能被六個因子包括的部分,稱為特殊因子 文獻來源...
驗證性因子分析是對社會調查數據進行的一種統計分析。它測試一個因子與相對應的測度項之間的關係是否符合研究者所設計的理論關係。驗證性因子分析往往通過結構方程建模...
正交因子模型(orthogonal factor model)是一種特殊的公共因子模型。正交因子模型的基本假設是:各個公共因子間相互獨立;各個特殊因子間相互獨立;各個公共因子與各個...
飛機的飛行運行強度用一個圖來表示,它的水平刻度是基於載荷因子的。這個圖稱為VG圖,速度-載荷圖(速度-載荷因子關係圖)。每一個飛機都有它自己的VG圖,它在特定...
一個電站不可能負荷就是發電機的容量,特別是新建的電站。通常像核電站設計的負荷因子為65%,國際水平也就85%左右詞條標籤: 科技術語 , 科學 V百科往期回顧 詞條...
《漫畫統計學之因子分析》是科學出版社出版的圖書,作者是高橋 信。本書是世界上最簡單的因子分析教科書,它通過漫畫式的情景說明,讓你邊看故事邊學知識,每讀完...
因子載荷反映指標對評價結果的影響程度,因子載荷絕對值越大表示指標對評價結果越重要,越應該保留;反之,越應該刪除。1通過對相關性分析篩選後的指標進行主成分分析,...
對應分析(Correspondence analysis)也稱關聯分析、R-Q型因子分析,是近年新發展起來的一種多元相依變數統計分析技術,通過分析由定性變數構成的互動匯總表來揭示變數間的...
對應分析也稱關聯分析、R-Q型因子分析,是近年新發展起來的一種多元相依變數統計分析技術,通過分析由定性變數構成的互動匯總表來揭示變數間的聯繫。可以揭示同一變數...
