共線性

共線性，即同線性或同線型。統計學中，共線性即多重共線性。

多重共線性（Multicollinearity）是指線性回歸模型中的解釋變數之間由於存在精確相關關係或高度相關關係而使模型估計失真或難以估計準確。

一般來說，由於經濟數據的限制使得模型設計不當，導致設計矩陣中解釋變數間存在普遍的相關關係。完全共線性的情況並不多見，一般出現的是在一定程度上的共線性，即近似共線性。

基本介紹

• 中文名：共線性
• 外文名：Collinearity
• 領域：統計學
• 依據模型：線性回歸模型
• 相關詞目：近似共線性

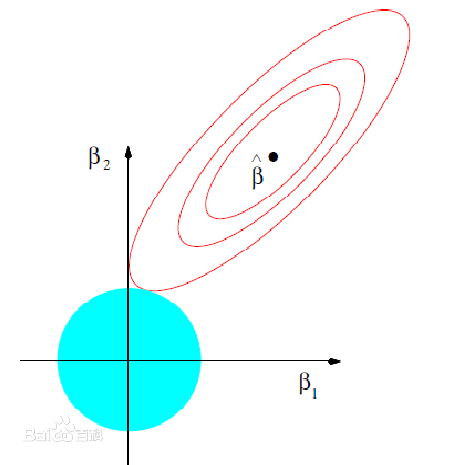
產生原因

主要有3個方面：

（1）經濟變數相關的共同趨勢。

（2）滯後變數的引入。

（3）樣本資料的限制。

影響

（1）完全共線性下參數估計量不存在。

（2）近似共線性下OLS估計量非有效。

多重共線性使參數估計值的方差增大，1/(1-r2)為方差膨脹因子(Variance Inflation Factor, VIF)如果方差膨脹因子值越大，說明共線性越強。相反 因為，容許度是方差膨脹因子的倒數，所以，容許度越小，共線性越強。可以這樣記憶：容許度代表容許，也就是許可，如果，值越小，代表在數值上越不容許，就是越小，越不要。而共線性是一個負面指標，在分析中都是不希望它出現，將共線性和容許度聯繫在一起，容許度越小，越不要，實際情況越不好，共線性這個“壞蛋”越強。進一步，方差膨脹因子因為是容許度倒數，所以反過來。總之就是找容易記憶的方法。

（3）參數估計量經濟含義不合理。

（4）變數的顯著性檢驗失去意義，可能將重要的解釋變數排除在模型之外。

（5）模型的預測功能失效。變大的方差容易使區間預測的“區間”變大，使預測失去意義。

需要注意：即使出現較高程度的多重共線性，OLS估計量仍具有線性性等良好的統計性質。但是OLS法在統計推斷上無法給出真正有用的信息。

判斷共線性的方法

表1.共線性判斷

共線性判斷
模型	維數	特徵值	條件索引	方差比例
				常量	人均國內生產水平	出生率	每個醫生平均負擔人口數
1	1	3.522	1	0	0	0	0
	2	0.459	2.771	0	0.15	0.15	0
	3	0.014	0.014	0.74	0.41	0.28	0
	4	0.006	0.006	0.26	0.44	0.72	0.99
a,因變數：老齡化水平（萬分之一）
b.僅選擇那些對於其分組（1為德國2為中國）=1的案例

如上表，是對德國人口老齡化情況的分析，其中y是老齡化情況，線性回歸的x1、x2、x3分別為人均國內生產總值、出生率、每個醫生平均負擔人口數。

判斷方法1：特徵值，存在維度為3和4的值約等於0，說明存在比較嚴重的共線性。

判斷方法2：條件索引列第3第4的值大於10，可以說明存在比較嚴重的共線性。

判斷方法3：比例方差記憶體在接近1的數（0.99），可以說明存在較嚴重的共線性。

解決方法

（1）排除引起共線性的變數。

找出引起多重共線性的解釋變數，將它排除出去，以逐步回歸法得到最廣泛的套用。

（2）差分法。

時間序列數據、線性模型：將原模型變換為差分模型。

（3）減小參數估計量的方差：嶺回歸法（Ridge Regression）。