基本介紹
- 中文名:一階線性微分方程
- 外文名:First order linear differential equation
- 定義:形如y'+P(x)y=Q(x)的微分
- 分類:當Q(x)≡0時,方程為y'+P(x)y=0
- 解法:一般用常數變易法
定義




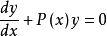


通解求法
一階齊次線性微分方程
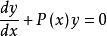
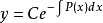
一階非齊次線性微分方程
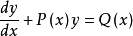
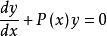
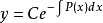








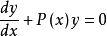


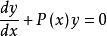
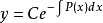
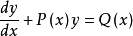
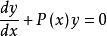
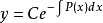



形如y'+P(x)y=Q(x)的微分方程稱為一階線性微分方程,Q(x)稱為自由項。一階,指的是方程中關於Y的導數是一階導數。線性,指的是方程簡化後的每一項關於y...
形如y'=f(y/x)的一階微分方程,稱為齊次一階微分方程。齊次微分方程是一個微分方程,如果它的一個解乘以任意常數後,仍是它的解,則稱為齊次微分方程。對一階...
線性常微分方程是微分方程中出現的未知函式和該函式各階導數都是一次的,稱為線性常微分方程。它的理論是常微分方程理論中基本上完整、在實際問題中套用很廣的一...
線性微分方程組(first order linear differentialequation system)是由幾個微分方程聯立起來共同確定幾個具有同一自變數的函式的情形.這些聯立的微分方程稱為微分方程組...
二階線性微分方程是指未知函式及其一階、二階導數都是一次方的二階方程,簡單稱為二階線性方程。二階線性微分方程的求解方式分為兩類,一是二階線性齊次微分方程,...
對於一元函式來說,如果在該方程中出現因變數的二階導數,我們就稱為二階(常)微分方程,其一般形式為F(x,y,y',y'')=0。在有些情況下,可以通過適當的變數...
n階線性常微分方程(linear differential equation of n-th order)是未知函式導數最高階數為n的線性常微分方程。...
一階低通濾波器的特性一般用一階線性微分方程表示。一般,線性連續系統的特性除了可以在“時域”中用微分方程或衝擊回響表示外,也可以用以頻率為自變數的函式表示,它...
這是一類具有非齊次項的線性微分方程,其中一階非齊次線性微分方程的表達式為y'+p(x)y=Q(x);二階常係數非齊次線性微分方程的表達式為y''+py'+qy=f(x)。...
本書是“21世紀高等學校經濟數學教材”叢書之一.全書共8章,內容分別為:緒論、初等積分法、一階常微分方程解的存在唯一性、高階微分方程、一階線性微分方程組、...
《常微分方程教程(第2版)》是作者在北京大學數學學院多年教學實踐的基礎上編寫而成的,第一版於1991年出版。作者在第二版準備的過程中,在力求保持原有風格、...
常數變易法是解線性微分方程行之有效的一種方法。它是拉格朗日十一年的研究成果,我們所用僅是他的結論,並無過程。...
