這是一類具有非齊次項的線性微分方程,其中一階非齊次線性微分方程的表達式為y'+p(x)y=Q(x);二階常係數非齊次線性微分方程的表達式為y''+py'+qy=f(x)。研究非齊次線性微分方程其實就是研究其解的問題,它的通解是由其對應的齊次方程的通解加上其一個特解組成。
基本介紹
- 中文名:非齊次線性微分方程
- 外文名:non-homogeneous lineardifferential equation
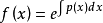






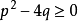












這是一類具有非齊次項的線性微分方程,其中一階非齊次線性微分方程的表達式為y'+p(x)y=Q(x);二階常係數非齊次線性微分方程的表達式為y''+py'+qy=f(x)。研究非齊次線性微分方程其實就是研究其解的問題,它的通解是由其對應的齊次方程的通解加上其一個特解組成。
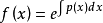






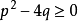












這是一類具有非齊次項的線性微分方程,其中一階非齊次線性微分方程的表達式為y'+p(x)y=Q(x);二階常係數非齊次線性微分方程的表達式為y''+py'+qy=f(x)。...
簡單來講,線性微分方程是指關於未知函式及其各階導數都是一次方,否則稱其為非線性微分方程。...
形如y'+P(x)y=Q(x)的微分方程稱為一階線性微分方程,Q(x)稱為自由項。一階,指的是方程中關於Y的導數是一階導數。線性,指的是方程簡化後的每一項關於y...
線性微分方程組(first order linear differentialequation system)是由幾個微分方程聯立起來共同確定幾個具有同一自變數的函式的情形.這些聯立的微分方程稱為微分方程組...
二階常係數線性微分方程是形如y''+py'+qy=f(x)的微分方程,其中p,q是實常數。自由項f(x)為定義在區間I上的連續函式,即y''+py'+qy=0時,稱為二階常...
6.1.1 齊次線性微分方程組 6.1. 2 非齊次線性微分方程組 6.2 常係數線性微分方程組 6.2.1 矩陣指數函式的定義和性質 6.2.2 常係數齊次線性微分方程組的...
二階線性微分方程是指未知函式及其一階、二階導數都是一次方的二階方程,簡單稱為二階線性方程。二階線性微分方程的求解方式分為兩類,一是二階線性齊次微分方程,...
定理2(線性非齊次微分方程通解的結構定理)如果y0是非齊次微分方程(1)的一個特解,而y*是對應的齊次微分方程(2)的通解,則y=y0+y*是方程(1)的通解。...
《非線性常微分方程邊值問題》是作者近年來研究工作的總結。在介紹拓撲度理論的...1.4.2 第二類半齊線性邊值問題的解1.4.3 非齊次線性邊值問題的解...
在常微分方程方面,一階方程中可求得通解的,除了線性方程、可分離變數方程和用...非齊次一階常係數線性微分方程:齊次二階線性微分方程:非齊次一階非線性微分方程...
n階線性常微分方程(linear differential equation of n-th order)是未知函式導數最高階數為n的線性常微分方程。...
是(2)的一個特解,Y是與(2)對應的齊次方程(1)的通解,那么是二階非齊次線性微分方程(2)的通解。(3)二階常係數齊次線性方程解法:二...
線性常微分方程是微分方程中出現的未知函式和該函式各階導數都是一次的,稱為線性常微分方程。它的理論是常微分方程理論中基本上完整、在實際問題中套用很廣的一...
線性偏微分方程是一類重要的偏微分方程,關於所有未知函式及其導數都是線性的偏微分方程稱為線性偏微分方程。例如,拉普拉斯方程、熱傳導方程及波動方程都是線性偏微分...
形如y'=f(y/x)的一階微分方程,稱為齊次一階微分方程。齊次微分方程是一個微分方程,如果它的一個解乘以任意常數後,仍是它的解,則稱為齊次微分方程。對一階...
常微分方程,學過中學數學的人對於方程是比較熟悉的;在初等數學中就有各種各樣的方程,比如線性方程、二次方程、高次方程、指數方程、對數方程、三角方程和方程組...
齊次方程(homogeneous equation)是數學的一個方程。指簡化後的方程中所有非零項的指數相等。也叫所含各項關於未知數的次數。其方程左端是含未知數的項,右端等於零...
3.5 微分方程的基本理論第四章 線性微分方程4.1 線性微分方程的一般理論4.2 常係數齊次線性微分方程4.3 常係數非齊次線性微分方程4.4 變係數線性向分方程...
通解結構定理(structure theorem of general solution)是一種關於線性常微分方程解的結構性質的數學表述。對於一個微分方程而言,其解往往不止一個,而是有一組,可以...
代入徑向運動方程 ,將此方程除以 ,則可得到一個簡單的常係數非齊次線性全微分方程來描述行星軌道:為了解這個微分方程,先列出一個特解...
