線性偏微分方程是一類重要的偏微分方程,關於所有未知函式及其導數都是線性的偏微分方程稱為線性偏微分方程。例如,拉普拉斯方程、熱傳導方程及波動方程都是線性偏微分方程。
基本介紹
- 中文名:線性偏微分方程
- 外文名:linear partial differential equation
- 所屬學科:數理科學
- 相關概念:偏微分方程、線性、偏導數等
- 舉例:拉普拉斯方程、熱擴散方程等
基本概念
定義
偏微分方程


基本性質
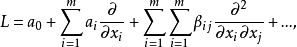

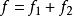
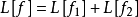
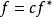


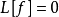



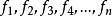
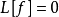
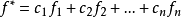

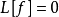
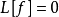
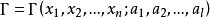
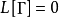

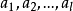
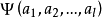


二階線性偏微分方程
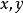

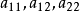
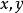
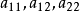

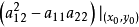
經典線性偏微分方程
波動方程

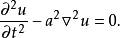

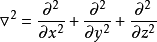
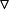

熱擴散方程
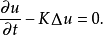
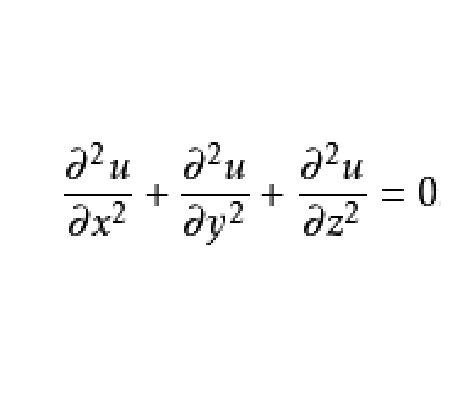
線性偏微分方程是一類重要的偏微分方程,關於所有未知函式及其導數都是線性的偏微分方程稱為線性偏微分方程。例如,拉普拉斯方程、熱傳導方程及波動方程都是線性偏微分方程。


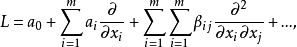

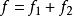
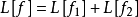
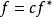


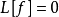



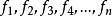
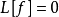
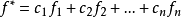

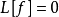
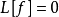
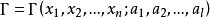
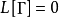

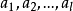
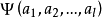



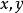
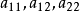

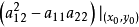

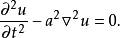

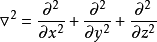

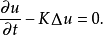
線性偏微分方程是一類重要的偏微分方程,關於所有未知函式及其導數都是線性的偏微分方程稱為線性偏微分方程。例如,拉普拉斯方程、熱傳導方程及波動方程都是線性偏微分...
簡單來講,線性微分方程是指關於未知函式及其各階導數都是一次方,否則稱其為非線性微分方程。...
非線性偏微分方程是各階微分項有次數高於一的微分方程即為非線性偏微分方程,是現代數學的一個重要分支,無論在理論中還是在實際套用中,非線性偏微分方程均被用來...
一階偏微分方程是最簡單的一類偏微分方程。一階偏微分方程的幾何理論有悠久的歷史淵源,以後經過É.(-J.)嘉當等人的發展,在幾何學、力學和物理學中都有重大的...
《線性偏微分方程講義》是2011年哈爾濱工業大學出版社出版的圖書,作者是L·尼倫伯格。...
包含未知函式的偏導數(或偏微分)的方程。方程中所出現未知函式偏導數的最高階數,稱為該方程的階。在數學、物理及工程技術中套用最廣泛的,是二階偏微分方程,習慣...
齊次一階線性偏微分方程:拉普拉斯方程,是橢圓型的齊次二階常係數線性偏微分方程:KdV方程, [3] 是三階的非線性偏微分方程:微分方程微分方程的解 編輯 微分方程的...
形如y'+P(x)y=Q(x)的微分方程稱為一階線性微分方程,Q(x)稱為自由項。一階,指的是方程中關於Y的導數是一階導數。線性,指的是方程簡化後的每一項關於y...
非線性偏微分方程的在物理學、氣動力學、流體力學、大氣物理、海洋物理、爆炸物理、化學、生理學、生物學、生態學等領域都有重要的套用。非線性偏微分方程的研究,...
《非線性偏微分方程的解析解》是在2012年山東人民出版社出版的圖書,作者是陳懷堂。本書主要介紹了非線性偏微分方程的解析。...
雙曲型偏微分方程是描述振動或波動現象的一類重要的偏微分方程。雙曲型偏微分方程解可以分解為振動與振動相乘,或指數函式與指數函式相乘的形式,一般能量無窮。...
概念定義 (linear elliptic partial differential equations of second order)一 類關於自變數二一(二;,二:,…,二。)的未知函式u(二) 的二階線性偏微分方程 當...
一階非線性偏微分方程(non-linear partial dif- ferential equation of first order)一階的完全非線 J勝偏微分方程.兩個自變數的一階非線性偏微分方 程的一般...
橢圓型偏微分方程,簡稱橢圓型方程,一類重要的偏微分方程。早在1900年D.希爾伯特提的著名的23個問題中,就有三個問題是關於橢圓型方程與變分法的。八十多年來,...
簡稱拋物型方程,一類重要的偏微分方程。熱傳導方程是最簡單的一種拋物型方程。 熱傳導方程研究熱傳導過程的一個簡單數學模型。根據熱量守恆定律和傅立葉熱傳導實驗...
偏微分方程論(theory of partial differential e- quations)指包含多元函式的偏導數等式的偏微分方程,描述自變數、未知函式及其偏導數之間的關係。符合這個關係的函式...
《實用偏微分方程》是2007年機械工業出版社出版的圖書,作者是哈伯曼。...... 波動方程和熱傳導方程的格林函式、線性和擬線性波動方程的特徵線法以及偏微分方程的拉普...
這是一類具有非齊次項的線性微分方程,其中一階非齊次線性微分方程的表達式為y'+p(x)y=Q(x);二階常係數非齊次線性微分方程的表達式為y''+py'+qy=f(x)。...
《套用偏微分方程》是浙江大學出版社出版的圖書,作者是王定江。本書講述了一階偏微分方程j及二階偏微分方程模型與分類。...
《偏微分方程基本理論》是2009年科學出版社出版的圖書,作者是王明新。...... 《偏微分方程基本理論》系統介紹了二階線性橢圓型方程、拋物型方程和雙曲型方程以及一...
常係數線性微分方程(組)( linear differentialequation (system) with constant coefficients)最簡單並可用代數方法求解的一類常微分方程(組)...
