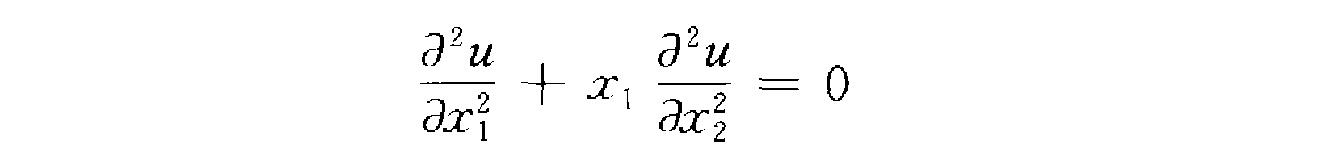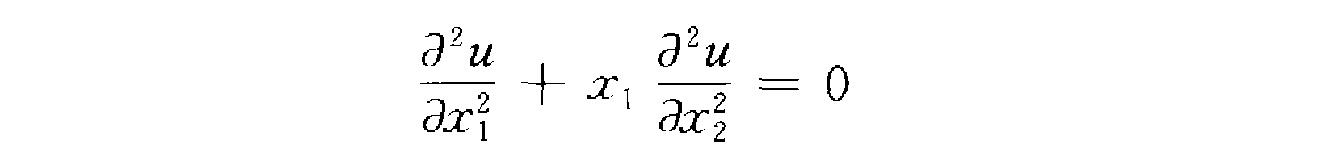概念定義
(linear elliptic partial differential equations of second order)一 類關於自變數二一(二;,二:,…,二。)的未知函式u(二) 的二階線性偏微分方程
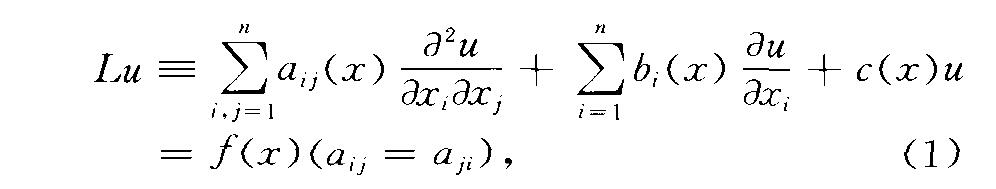
當其係數矩陣(a;;(二))在域f2的各點x上都是正定 時,就稱橢圓型運算元L或方程(<1)在月中為橢圓型 的;即如果用幾(二),n(x)分別表示係數矩陣(a;;(二)) 的最小和最大特徵值,那么
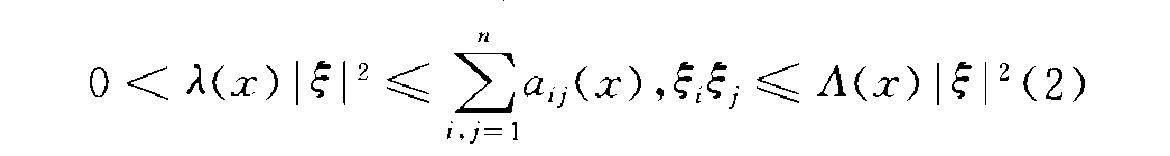
對於所有的s}=<s}ms}Z}...,s}n>ER"\}o}和二E}成 立.如果對於某常數隻。有}(x) i}o>o(dx任f2),就 稱橢圓型運算元1或方程((1)在f2中是強橢圓型的. 如果n(二)在f2中有界,則稱橢圓型運算元L或方程 (1)為嚴格橢圓型的.如果n(二)/.1(x)在口中有界, 則稱運算元L或方程(1>是一致橢圓型的.存在偏微 分方程是橢圓型的而不是一致橢圓型的
,例如兩個 自變數的二階偏微分方程 在半平面二1>o中是橢圓型的而不是一致橢圓型 的,但它在條形區域((a,戶XR‘中(這裡
是一致橢圓型的.調和方程是最簡單最典型的 二階橢圓型偏微分方程.