簡稱拋物型方程,一類重要的偏微分方程。熱傳導方程是最簡單的一種拋物型方程。 熱傳導方程研究熱傳導過程的一個簡單數學模型。根據熱量守恆定律和傅立葉熱傳導實驗定律導致熱傳導方程。
基本介紹
- 中文名:拋物型偏微分方程
- 外文名:system of parabolic partial differential equations
- 簡稱:拋物型方程
- 類別:重要的偏微分方程
- 種類:熱傳導方程
定義
二階拋物線方程組

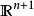


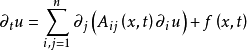
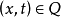
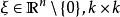

高階拋物型方程組
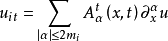





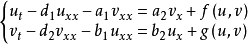

簡稱拋物型方程,一類重要的偏微分方程。熱傳導方程是最簡單的一種拋物型方程。 熱傳導方程研究熱傳導過程的一個簡單數學模型。根據熱量守恆定律和傅立葉熱傳導實驗定律導致熱傳導方程。

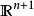


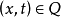
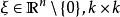

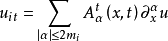





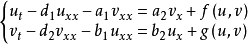
簡稱拋物型方程,一類重要的偏微分方程。熱傳導方程是最簡單的一種拋物型方程。 熱傳導方程研究熱傳導過程的一個簡單數學模型。根據熱量守恆定律和傅立葉熱傳導實驗...
二階線性拋物型方程(linear parabolic equation of second order)是最重要的一類拋物型方程,全稱是二階線性拋物型偏微分方程。關於未知函式u(x1,x2,…,xn)的偏...
包含未知函式的偏導數(或偏微分)的方程。方程中所出現未知函式偏導數的最高階數,稱為該方程的階。在數學、物理及工程技術中套用最廣泛的,是二階偏微分方程,習慣...
線性偏微分方程是一類重要的偏微分方程,關於所有未知函式及其導數都是線性的偏微分方程稱為線性偏微分方程。例如,拉普拉斯方程、熱傳導方程及波動方程都是線性偏微分...
本書是為高等院校計算數學專業高年級本科生和研究生偏微分方程數值解法課程編寫的教材。全書分為差分方法和有限元方法兩個相互獨立的部分。差分方法部分的先修課程...
《偏微分方程數值解法第2版》是2004年清華大學出版社出版的圖書,作者是陸金甫、關治,...
《偏微分方程與數值方法》是2006年科學出版社出版的圖書,作者是拉松。...... 分別用三章闡述橢圓型、拋物型及雙曲型偏微分方程,一章關於其數學理論,一章關於其有...
《偏微分方程數值解法》根據教育部專業目錄調整後的要求及計算數學的發展,在筆者修訂版《微分方程數值解法》的基礎上編寫而成。全書包括六章,第一、二章是變分形式...
《偏微分方程數值解法(第3版)》是2016年清華大學出版社出版的書籍,作者是陸金甫、關治。...
混合型偏微分方程(partial differential equation of mixed type),簡稱混合型方程,一偏微分方程在所考慮的區域的某一部分上是橢圓型的,在另一部分上是雙曲型的,...
《偏微分方程基本理論》是2009年科學出版社出版的圖書,作者是王明新。...... 《偏微分方程基本理論》系統介紹了二階線性橢圓型方程、拋物型方程和雙曲型方程以及一...
《現代偏微分方程導論》是2007年10月1日科學出版社出版的圖書,作者是陳恕行。本書主要講述偏微分方程的一般理論、廣義函式與Sobolev空間、橢圓邊值問題、能量方法、...
拋物型控制系統(controlled system governedby parabolic partial differential equation)一類由拋物型偏微分方程描述的分布參數控制系統.設月是R"中的區域,其邊界r是...
《雙非線性拋物型方程解的長時間行為》是一篇論文,作者是李永軍,導師是鐘承奎。...... 拋物型方程 非線性方程 偏微分方程 吸引子 數值解館藏號O175.26...
《偏微分方程並行算法及反問題數值解法》是2015年清華大學出版社出版的圖書,作者劉春鳳、彭亞綿。...
《偏微分方程的調和分析方法》是2008年科學出版社出版的圖書,作者是苗長興,張波 。...... 拋物型方程的時空估計方法、Littlewood-Paley理論與不可壓Navier-Stokes方程...
偏微分方程初值問題差分法是一種求解偏微分方程初值問題和初邊值問題的主要數值方法。...
《偏微分方程的MATLAB解法》,是武漢大學出版社2011年出版的圖書。...... 本書詳細介紹了MATLAB6的偏微分方程工具箱,...1 求解橢圓型方程的例子2 求解拋物型方程的...
《科學計算中的偏微分方程有限差分法》是高等教育出版社2006-6-1出版的圖書。...... 內容包括科學計算中典型的橢圓型方程、雙曲型方程和拋物型方程的差分格式構造...
菲克第二定律是在第一定律的基礎上結合質量守恆方程推導出來的,預測了擴散導致濃度隨時間的變化,是一個拋物型偏微分方程。...
