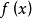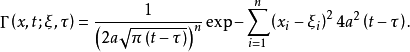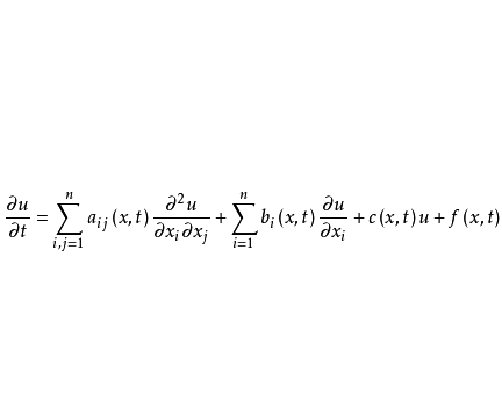二階線性拋物型方程(linear parabolic equation of second order)是最重要的一類拋物型方程,全稱是二階線性拋物型偏微分方程。關於未知函式u(x1,x2,…,xn)的偏微分方程是一個含有u(x1,x2,…,xn)的偏導數的等式,其中最高階偏導數的階數稱為該方程的階。線性、非線性偏微分方程的意義與常微分方程相應的概念相類似。
基本介紹
- 中文名:二階線性拋物型方程
- 外文名:linear parabolic equation of second order
- 所屬學科:數學
- 所屬問題:偏微分方程(拋物型方程)
基本介紹,二階線性拋物型方程的基本解,
基本介紹
二階線性拋物型方程是最重要的一類拋物型方程,對於二階線性偏微分方程
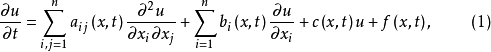





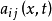
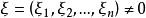

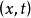



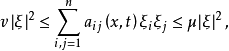

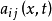


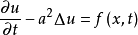
二階線性拋物型方程的基本解
二階線性拋物型方程的基本解是二階線性拋物型方程的一種具有奇性的特解,二階線性拋物型方程 在
在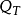 中的基本解是一個對一切
中的基本解是一個對一切 都有定義的函式
都有定義的函式 ,它滿足如下條件:
,它滿足如下條件:

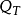


1. 對固定的 ,作為
,作為 的函式在域
的函式在域 中滿足方程
中滿足方程 。
。




2. 對每一個在 上連續的函式
上連續的函式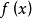 ,當
,當 時有
時有