等積仿射變換

等積仿射變換亦稱麼模仿射變換，是一種特殊的仿射變換，指變積係數的絕對值等於1的仿射變換。

基本介紹

• 中文名：等積仿射變換
• 所屬學科：數學
• 別稱：麼模仿射變換
• 所屬問題：高等幾何(仿射幾何)
• 簡介：變積係數的絕對值是1的仿射變換

基本介紹

仿射變換(affine transformation)是歐氏空間中的一種變換。在仿射坐標系下如果一個變換使得坐標為的任意點變換成坐標為的點，其中

這裡是常數，且，則稱此變換為仿射變換。當時稱為等積仿射變換。仿射變換的全體組成群，稱為仿射變換群。仿射變換最基本的性質是把任意共線的三點變換為共線的三點。

相關分析

今有兩個相異或非相異平面[P]和[P’]，其上面的點分別按坐標系XOY和X'O'Y'‘定位。這兩個平面上對應點之間的一一對應變換叫做單應變換或直射變換，它由以下齊次坐標關係式

確定，且變換的行列式不等於零，即

行列式叫做變換的模。

如果解出方程組(1)的x、y、z，則得到與從平面P'變換到平面P相似的公式，而且在所得的公式中相應的係數是行列式(2)的代數餘子式。

我們考慮到平面P與P’的無窮遠直線在仿射變換中也是互相對應的，故可得，用非齊次坐標表示此變換，則為

並有行列式

平面P上共線三點M₁、M₂、M₃的仿射對應元素同樣是共線的三點M'₁、M'₂、M'₃，而且它們的簡比不變，即

仿射變換的平行性不變，成仿射對應的圖形的面積比是常數。換個說法，若某圖形F的仿射對應圖形是F‘，則

面積F’=面積F

式中的是變換的行列式。如果

這個變換叫做么模仿射變換或等積仿射變換，就是說在變換中圖形面積保持原來的大小。

如果變換的模是正值，則兩個圖形的形態和外輪廓線畫成同方向的。這種情況下的仿射變換叫做直接仿射變換。

如果變換的模是負值，則仿射變換叫做間接的或逆向變換，兩個圖形輪廓畫成異向的。

仿射變換構成一個含有六個參數的變換群，而等積仿射變換構成一個含有五個參數的變換群。

為了弄清仿射變換的幾何意義，我們在平面P上建立笛卡爾坐標系XOY。平面上一點U的坐標是(1，1)，稱它為單位點。平面P上任意點M有坐標

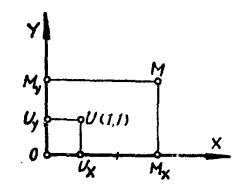式中M_x與M_y是M點在OX軸和OY軸上的投影(圖1)。

圖1

圖2

如果將平面P仿射變換到平面P'，則取笛卡爾坐標系XOY，並變換為X'O'Y'，U點相M點變換為對應點U’和M‘。在新坐標系裡取U‘力單位點，其度量單位在O’X'軸上取，在軸上取(圖2)，變換前後的兩種度量單位不同。

按照這種方式把M點變換為M’點，它在坐標系O'X’Y’中的坐標為

因為在仿射變換中簡比是不變數，所以

笛卡爾坐標的仿射變換就是這個等式的推廣，因為各軸的度量單位是不同的。

在仿射變換中，新得到的坐標系仍是仿射坐標系。