泛函分析中一種重要的運算元。
運算元(映射)有線性和非線性之分.線性運算元又分為有界和無界兩類,有界線性運算元是線性賦范空問的基本概念。
基本介紹
- 中文名:有界線性運算元
- 外文名:bounded linear operator
- 所屬領域:數理科學
- 反義詞:無界線性運算元
基本定義



舉例
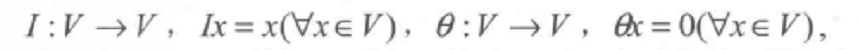


相關概念
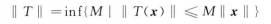


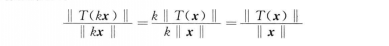
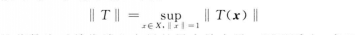
相關定理

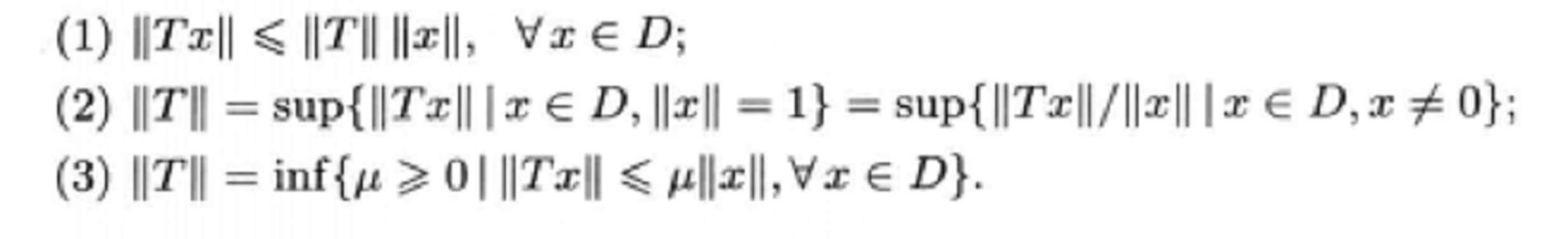
等價形式








泛函分析中一種重要的運算元。
運算元(映射)有線性和非線性之分.線性運算元又分為有界和無界兩類,有界線性運算元是線性賦范空問的基本概念。



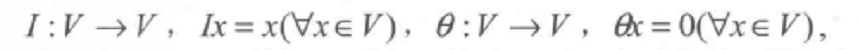


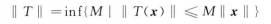


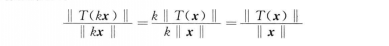
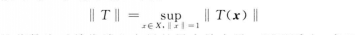

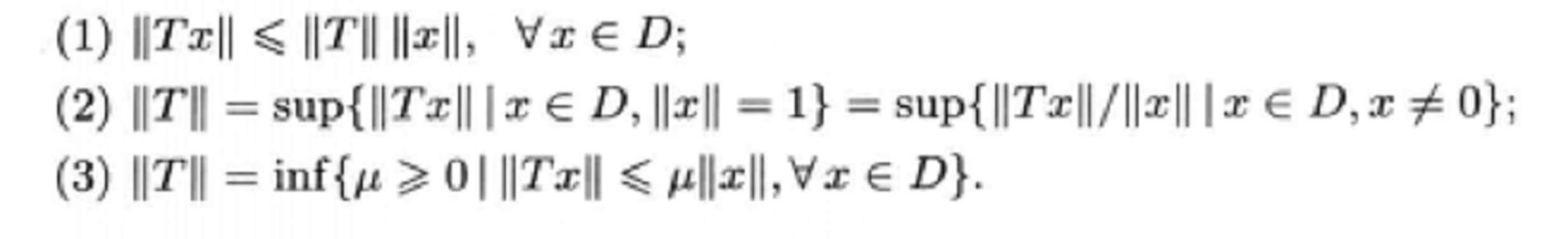







泛函分析中一種重要的運算元。運算元(映射)有線性和非線性之分.線性運算元又分為有界和無界兩類,有界線性運算元是線性賦范空問的基本概念。...
有界n線性運算元是映有界集的n線性運算元。n線性運算元的有界性與連續性是等價的。...... 有界n線性運算元是映有界集的n線性運算元。n線性運算元的有界性與連續性是等價...
相似線性運算元(similar linear operator)是相似矩陣的推廣,相似運算元具有相同的譜。...... 設A,B是巴拿赫空間上的有界線性運算元,如果存在可逆的有界運算元W(即W,W-1...
共軛線性運算元(conjugate linear operator)是由線性運算元誘導出的共軛空間之間的運算元。...
線性算字,我們稱它為線性映射、線性運算元或線性變換。...... 1。一個有界線性運算元是一致連續的。若一個線性運算元在一點連續, 則它是有界的。2。所有賦范向量空...
)上的兩個賦范向量空間。從U到V的線性運算元被稱為有界,如果存在C>0滿足對所有x U。有界運算元構成一個向量空間。在這個向量空間上,我們可以引入一個與U和V的范...
初等運算元是運算元代數上一類重要的線性映射,是連結運算元理論和運算元代數理論的橋樑。...... 廣義導運算元是對所有有界線性運算元定義的一種運算。設𝓑(X)表示巴拿赫空間X ...
弗雷德霍姆運算元是可逆運算元的推廣。設T是希爾伯特空間H上的有界線性運算元,即T∈𝓑(H),如果T的值域𝓡(T)是閉的且 則稱T是弗雷德霍姆運算元,稱 為T的指標數。...
所謂有界線性運算元空間,是指賦范線性空間X到賦范線性空間Y的有界線性運算元全體。...... 有界線性運算元是線性賦范空問的基本概念,是泛函分析中一種重要的運算元。...
設A是賦范線性空間X到賦范線性空間Y的有界線性運算元,如果值域𝓡(A)是Y的有限維線性子空間,則稱A是有限秩運算元。...
第一章Hilbert空間上運算元的一般理論 1.1Banach空間上的有界線性運算元 1.1.1Banach空間及其共軛空間 1.1.2Banach空間上的有界線性運算元及其共軛運算元 1.2Hilbert...
本書從有限維空間線性運算元的特徵值出發,採用類比、歸納等方式,通過大量實例循序漸進地引入無窮維空間上線性運算元的譜理論,系統介紹並分析了有界線性運算元、共軛運算元、...
線性寬度是用線性運算元逼近代替最佳逼近的寬度。寬度是描述一個函式類“寬狹”的數量特徵。...
滿射線性運算元亦稱為映到上的線性運算元,是值域等於全空間的線性運算元。...... 到E上的一對一滿射的線性運算元,而且λI-T的逆運算元(λI-T)-1是E到E的有界線性運算元...
當H是有限維空間時,每個線性運算元都是跡類的,並且A的跡的定義與矩陣的跡的...如果A有界且B是跡類的,則AB和BA也是跡類的,且有此外,在同樣的假設下最後的...
是L2(Ω,𝓑,μ)到自身的有界線性運算元。希爾伯特-施密特積分運算元定義 如果L2(Ω,𝓑,μ)是可分空間,那么易知T是L2(Ω,𝓑,μ)上的希爾伯特-施密特運算元。因...
強運算元拓撲(strong operator topology)是運算元空間中的又一種拓撲。從賦范線性空間X到賦范線性空間Y的有界線性運算元全體所成的賦范線性空間B(X→Y)中由半范族{...
在數學中,矩陣或者有界線性運算元的譜半徑是指其特徵值絕對值集合的上確界,一般若為方陣A的譜半徑則寫作ρ(A)。...
在泛函分析中,巴拿赫定理是一個極為重要的工具。它允許了定義在某個向量空間上的有界線性運算元擴張到整個空間,並說明了存在“足夠”的連續線性泛函,定義在每一個賦...
《泛函分析講義》是2011年科學出版社出版的圖書,作者是黎永錦。該書講述了度量空間、賦范線性空間、有界線性運算元等方面的知識。...
