在泛函分析中,巴拿赫定理是一個極為重要的工具。它允許了定義在某個向量空間上的有界線性運算元擴張到整個空間,並說明了存在“足夠”的連續線性泛函,定義在每一個賦范向量空間,使對偶空間的研究變得有趣味。
這個定理以漢斯·哈恩和斯特凡·巴拿赫命名,他們在1920年獨立證明了這個定理。
基本介紹
- 中文名:巴拿赫定理
- 外文名:Hahn–Banach theorem
- 學科:數學
內容簡介
表述
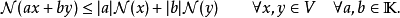
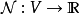
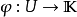
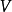
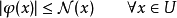
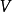
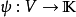

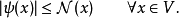
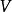
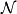
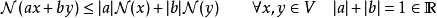

在泛函分析中,巴拿赫定理是一個極為重要的工具。它允許了定義在某個向量空間上的有界線性運算元擴張到整個空間,並說明了存在“足夠”的連續線性泛函,定義在每一個賦范向量空間,使對偶空間的研究變得有趣味。
這個定理以漢斯·哈恩和斯特凡·巴拿赫命名,他們在1920年獨立證明了這個定理。
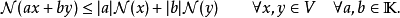
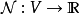
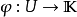
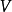
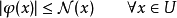
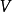
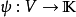

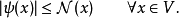
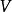
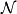
在泛函分析中,巴拿赫定理是一個極為重要的工具。它允許了定義在某個向量空間上的有界線性運算元擴張到整個空間,並說明了存在“足夠”的連續線性泛函,定義在每一個賦...
在泛函分析中,哈恩-巴拿赫定理是一個極為重要的工具。它允許了定義在某個向量空間上的有界線性運算元擴張到整個空間,並說明了存在「足夠」的連續線性泛函,定義在每...
波蘭數學家。1892年3月30日生於克拉科夫,1945年8月31日卒於利沃夫。巴拿赫曾在克拉科夫的買吉洛尼亞大學和利沃夫工業大學短期學習,但他主要靠自學。1920年獲博士...
海因一巴拿赫定理(Hahn-Banach theorem)凸集幾何的基本定理.它是關於凸集與超平面的定理.它在泛函分析中有重要的套用,其關鍵乃是超平面與線性形式之間有著對應關係....
巴拿赫-塔斯基定理(或稱豪斯多夫-巴拿赫-塔斯基定理,又名“分球怪論”),是一條數學定理。1924年斯特凡·巴拿赫和阿爾弗雷德·塔斯基首次提出這一定理。這一定理...
巴拿赫-阿勞格魯定理是關於共軛空間中閉單位球是弱∗緊的重要定理。...... 巴拿赫-阿勞格魯定理是關於共軛空間中閉單位球是弱∗緊的重要定理。設X是巴拿赫空間,...
巴拿赫-薩克斯定理是關於算術平均收斂的一個定理。巴拿赫(Banach,S.)與薩克斯(Saks,S.)於1930年證明了1<p<+∞時定理成立。...
巴拿赫逆運算元定理(Banach inverse operator)是關於有界逆運算元存在的定理。...... 巴拿赫逆運算元定理(Banach inverse operator)是關於有界逆運算元存在的定理。...
在數學分析中,巴拿赫極限(英語:Banach limit)指的是定義在全體有界復序列組成的巴拿赫空間上,對每個巴拿赫空間中的序列和複數滿足一定條件的連續線性泛函。...
在數學中,反函式定理給出了向量值函式在含有定義域中一點的開區域內具有反函式的充分條件。該定理還說明了反函式的全導數存在,並給出了一個公式。反函式定理可以...
巴拿赫(Stefan Banach,公元1892年3月30日─公元1945年8月31日)是著名的波蘭數學家。生於克拉科夫,卒於利沃夫。...
此外,泛函分析中大部分重要定理都構建與罕-巴拿赫定理的基礎之上,而該定理本身就是選擇公理(Axiom of Choice)弱於布倫素理想定理(Boolean prime ideal theorem)的...
