基本介紹
- 中文名:矩陣運算元
- 外文名:Matrix Operator
- 領域:數學
運算元

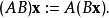
有界運算元和運算元範數
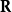



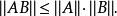
特殊情形
泛函
線性運算元
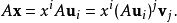
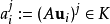




例子
幾何
機率論
微積分
標量和向量場上的基本運算元

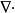
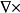
另請參閱
- 數學符號表
- 運算元代數
- 運算元列表
- 運運算元(編程)

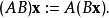
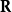



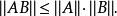
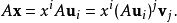
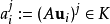
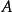
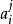



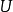


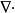
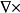
運算元(英語:Operator)是從一個向量空間(或模)到另一個向量空間(或模)的映射。矩陣運算元是當需要建立從當前矩陣到特殊類型矩陣的映射時所使用的方法。...
當需要建立從當前矩陣到特殊類型矩陣的映射時,就用到線性運算元的矩陣(簡稱運算元矩陣)。例如從矩陣到對角矩陣的變換,用到相似變換矩陣。...
在數學中,矩陣(Matrix)是一個按照長方陣列排列的複數或實數集合,最早來自於方程組的係數及常數所構成的方陣。這一概念由19世紀英國數學家凱利首先提出。矩陣是高等...
拉普拉斯矩陣(Laplacian matrix) 也叫做導納矩陣、基爾霍夫矩陣或離散拉普拉斯運算元,主要套用在圖論中,作為一個圖的矩陣表示。...
在數學裡,作用於一個有限維的內積空間,一個自伴運算元(self-adjoint operator)等於自己的伴隨運算元;等價地說,表達自伴運算元的矩陣是埃爾米特矩陣。埃爾米特矩陣等於自己...
矩陣範數(matrix norm)是數學中矩陣論、線性代數、泛函分析等領域中常見的基本概念,是將一定的矩陣空間建立為賦范向量空間時為矩陣裝備的範數。套用中常將有限維賦...
索伯運算元(Sobel operator)是圖像處理中的運算元之一,有時又稱為索伯-費德曼運算元或索貝濾波器,在影像處理及電腦視覺領域中常被用來做邊緣檢測。索伯運算元最早是由艾...
拉普拉斯運算元(Laplace Operator)是n維歐幾里德空間中的一個二階微分運算元,定義為梯度(▽f)的散度(▽·f)。拉普拉斯運算元也可以推廣為定義在黎曼流形上的橢圓型運算元,...
矩陣拉直運算(matrix vec operator)是處理矩陣的一種方法。...... 矩陣拉直運算(matrix vec operator)是處理矩陣的...稱vec為按列拉直運算元.基拉直後的vec(基)是一...
Sobel運算元是像素圖像邊緣檢測中最重要的運算元之一,在機器學習、數字媒體、計算機視覺等信息科技領域起著舉足輕重的作用。在技術上,它是一個離散的一階差分運算元,用來...
索貝爾運算元是計算機視覺領域的一種重要處理方法。主要用於獲得數字圖像的一階梯度,常見的套用和物理意義是邊緣檢測。索貝爾運算元是把圖像中每個像素的上下左右四領域的...
在頻域中的乘積運算元或在時域中的卷積運算元在Hankel和特普利茨(Toeplitz)運算元的發展中扮演了一個重要的角色。事實上,乘積運算元可分解成若干Hankel和特普利茨(Toeplitz)...
用來產生圖像邊緣增強效果的運算單元。取2×2或3×3的矩陣。當取2×2矩陣時,可增強被該運算單元所覆蓋區域的左上角像素與周圍像素間的灰度差,當取3×3矩陣時...
巴拿赫空間上具有某種譜分解性質的一類運算元,它是若爾當型矩陣在無窮維空間的一種推廣。 自共軛的常微分方程的邊值問題的研究發展成希爾伯特空間上自伴運算元(或自共軛...
Q矩陣(62-matrix)標準轉移機率矩陣對應的轉移強度矩陣。...... (t))的Q矩陣.它是相應的轉移矩陣(或者說,馬爾可夫鏈)的轉移強度矩陣(又稱密度矩陣或無窮小運算元)...
Laplacian 運算元是n維歐幾里德空間中的一個二階微分運算元,定義為梯度grad的散度div。可使用運算模板來運算這定理定律。...
《分塊運算元矩陣譜理論及其套用》由科學出版社出版...... 《分塊運算元矩陣譜理論及其套用》以2×2分塊運算元矩陣的譜分析為主線,對分塊運算元矩陣的一些最基本的結構和...
《矩陣理論》,是2006年科學出版社出版的圖書,作者是蘇育才、姜翠波、張躍輝。主要介紹線性空間與線性變換、內積空間與等距變換、特徵值與特徵向量、λ-矩陣與Jordan...
使問題從一種狀態變化為另一種狀態的手段稱為操作符或算符。算符在單獨存在時是沒有什麼意義。操作符可為走步、過程、規則、數學運算元、運算符號或邏輯符號等。...
在數學裡,作用於一個有限維的內積空間,一個自伴運算元(self-adjoint operator)等於自己的伴隨運算元;等價地說,表達自伴運算元的矩陣是埃爾米特矩陣。即厄米算符表達了一...
在數學中,矩陣或者有界線性運算元的譜半徑是指其特徵值絕對值集合的上確界,一般若為方陣A的譜半徑則寫作ρ(A)。...
