賦范代數,是泛函分析的一個重要分支,研究帶有乘法的賦范線性空間的性質及其套用。
設A是賦范線性空間,如果在A上定義了乘法,即對於A中任何兩個元素x,y,對應有A中的一個元,稱為x與y的乘積,並記為xy。而且乘法具有下列性質:①(xy)z=x(yz);②α(xy)=(αx)y=x(αy);③(x+y)z=xz+yz;④z(x+y)=zx+zy,則稱A是賦范代數。
基本介紹
- 中文名:賦范代數
- 外文名:Normed algebra
- 所屬:泛函分析
- 意義:研究賦范線性空間的性質
定義
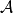
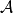
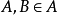
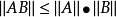
巴拿赫代數
簡介

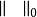
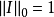
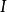
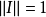

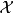
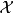
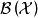
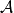

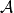
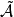
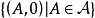
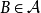

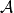

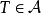





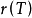
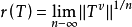


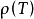

賦范代數,是泛函分析的一個重要分支,研究帶有乘法的賦范線性空間的性質及其套用。
設A是賦范線性空間,如果在A上定義了乘法,即對於A中任何兩個元素x,y,對應有A中的一個元,稱為x與y的乘積,並記為xy。而且乘法具有下列性質:①(xy)z=x(yz);②α(xy)=(αx)y=x(αy);③(x+y)z=xz+yz;④z(x+y)=zx+zy,則稱A是賦范代數。
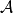
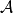
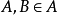
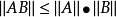
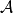
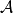

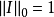
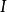
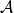
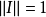
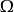

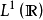
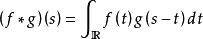
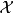
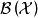
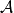

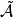
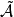
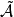
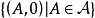
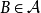

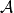
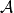

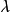

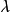
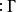




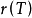
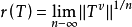


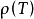
賦范代數,是泛函分析的一個重要分支,研究帶有乘法的賦范線性空間的性質及其套用。設A是賦范線性空間,如果在A上定義了乘法,即對於A中任何兩個元素x,y,對應有A...
完備的賦范代數稱為巴拿赫代數(Banach代數),它是泛函分析的一個重要分支,主要研究帶有乘法的賦范線性空間的性質及其套用。...
一個完備擬賦范向量空間被稱為擬巴拿赫空間。一個擬賦范空間{\displaystyle (A,\|\cdot \|)}被稱為擬賦范代數,如果向量空間A是一個代數且存在常數K>0滿足...
在通常的套用中,例如在函式空間中,它們有一個代數結構,即構成一個線性空間,同時還與某種收斂性相聯繫,處理這種結構最常用的一般方法是引入一個範數,這樣就導致賦...
巴拿赫代數常簡稱為B代數,是定義了乘法運算並滿足一定條件的復巴拿赫空間。設R是復賦范線性空間且R同時又是環,如果R中任何兩個元素x,y的乘積xy的範數滿足不等式...
賦范線性空間(normed linear space)是線上性空間中引進一種與代數運算相聯繫的度量,即由向量範數誘導出的度量。賦范線性空間稱為Banach空間,是指由範數導出的度量...
巴拿赫代數常簡稱為B代數,是定義了乘法運算並滿足一定條件的復巴拿赫空間。設R是復賦范線性空間且R同時又是環,如果R中任何兩個元素x,y的乘積xy的範數滿足不等式...
若 R具有賦范代數結構,則球面 S為H空間。這後一結論又等價於存在霍普夫不變數等於 1的球面映射S→S。 這個問題在同倫論發展的初期就被提出來,當時是個很難下...
1 概念 2 賦范線性空間 3 拉東-尼科迪姆性質 4 巴拿赫空間 5 巴拿赫代數 一致凸賦范線性空間概念 編輯 一致凸賦范線性空間(uniformly convexnormed linear spa...
商賦范線性空間是由賦范線性空間與其閉子空間誘導出的新的賦范線性空間。...... 賦范線性空間(normed linear space)是線上性空間中引進一種與代數運算相聯繫的度...
1940年,蓋爾范德獲蘇聯物理數學科學博士學位,在學位論文中,他創建了賦范環論,即巴拿赫代數論。 1943年,蓋爾范德開創了 C *代數的研究並開始擔任莫斯科大學教授。 ...
擬可逆元巴拿赫代數 編輯 完備的賦范代數稱為巴拿赫代數(Banach代數),它是泛函分析的一個重要分支,主要研究帶有乘法的賦范線性空間的性質及其套用。...
巴拿赫代數常簡稱為B代數,是定義了乘法運算並滿足一定條件的復巴拿赫空間。設R是復賦范線性空間且R同時又是環,如果R中任何兩個元素x,y的乘積xy的範數滿足不等式...
2.1.2 賦范代數2.1.3 Banach代數中元素的譜2.2 線性運算元的譜2.2.1 線性運算元譜的概念2.2.2 線性運算元譜的分類2.2.3 近似譜點2.2.4 共軛運算元及共軛...
任何具有這一性質的辛賦范代數被稱為Banach代數。 可以將譜理論推廣到這樣的代數上。C*-代數是具有一些附加結構的Banach代數,在量子力學中起重要作用。 [1] ...
17.1 賦范代數17.2 函式演算第18章 交換Banach代數的Gelfand理論第19章 交換Banach代數的Gelfand理論的套用19.1 代數C(S)19.2 Gelfand緊化...
2.1.2 賦范代數 2.1.3 Banach 代數中元素的譜 § 2.2 線性運算元的譜 2.2.1 線性運算元譜的概念 2.2.2 線性運算元譜的分類 2.2.3 近似譜點 2.2.4 ...
