線上性代數、泛函分析和數學的相關領域,擬範數與範數類似。
基本介紹
- 中文名:擬賦范空間
- 外文名:Quasi-ordination space
- 分類:數理科學
定義
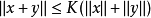

相關概念


線上性代數、泛函分析和數學的相關領域,擬範數與範數類似。
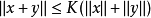



一個賦有擬範數的向量空間被稱為擬賦范向量空間。一個完備擬賦范向量空間被稱為擬巴拿赫空間。一個擬賦范空間{\displaystyle (A,\|\cdot \|)}被稱為擬賦...
賦準范線性空間(paranormed linear space)又稱為賦擬范線性空間,簡稱賦準范空間。...... 賦準范線性空間(paranormed linear space)又稱為賦擬范線性空間,簡稱賦...
《巴拿赫空間引論(第2版)》共九章,敘述泛函分析的最基本的內容。第一、二章是全書的基礎,討論賦范線性空間和線性運算元的基本概念;第三、四、五章是《巴拿赫空間...
擬逆元巴拿赫代數 編輯 完備的賦范代數稱為巴拿赫代數(Banach代數),它是泛函分析的一個重要分支,主要研究帶有乘法的賦范線性空間的性質及其套用。...
擬線性化方法巴拿赫空間 編輯 完備的賦范線性空間被稱為巴拿赫空間,是泛函分析研究的基本內容之一。20世紀以來,當人們研究了許多具體的無限維空間及其上面相應的收斂...
本書共有兩部分,第一部分的主要內容可以作為泛函分析的入門教材,我們在前兩章介紹和討論了賦范、賦準范和賦擬范空間及其上的線性運算元的基本概念,第三章介紹和...
擬可逆元巴拿赫代數 編輯 完備的賦范代數稱為巴拿赫代數(Banach代數),它是泛函分析的一個重要分支,主要研究帶有乘法的賦范線性空間的性質及其套用。...
擬相似線性運算元有界線性運算元 編輯 有界線性運算元是泛函分析中一種重要的運算元。設 是從線性賦范空間 到 的線性運算元。 如果 當存在且有限,則稱 是有界線性運算元,...
擬冪零運算元簡介 編輯 擬冪零運算元是冪零運算元概念的推廣,又稱為廣義冪零運算元。賦范線性空間上有界線性運算元T稱為擬冪零運算元,如果擬冪零運算元性質 編輯 ...
《泛函分析新講》是一本定光桂編制,由科學出版社在2007年出版的書籍。本書講述了賦范空間、賦準范空間和賦擬范空間等知識。...
