擬可逆元

在巴拿赫代數中引進運算x∘y=x+y-xy，當x∘y=0（或y∘x=0）時，稱y為x的右（或左）逆元，而稱x為擬可逆的。

基本介紹

• 中文名：擬可逆元
• 外文名：quasi-invertible element
• 適用範圍：數理科學

簡介

擬可逆元是巴拿赫代數中的一個概念。

在巴拿赫代數中引進運算

當（或）時，稱y為x的右（或左）逆元，而稱x為擬可逆的。

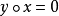
推論

設R有單位元e，y是x的擬逆元，則e-y就是e-x的逆元。可逆元稱為正則的，非可逆元稱為奇異的。

當複數λ滿足|λ|>||x||時，λ-x有擬逆元y，它由收斂級數給出，所有使λ-x不具有擬逆元的λ所成的集合稱為x的譜，記為Sp(x)。

當x本身無逆元，特別當R不含單位元時，恆有0∈Sp(x)。

巴拿赫代數

完備的賦范代數稱為巴拿赫代數（Banach代數），它是泛函分析的一個重要分支，主要研究帶有乘法的賦范線性空間的性質及其套用。

設X是賦范線性空間，則（由X到X的有界線性運算元全體）是一個有單位元的賦范代數，X上的恆等運算元I 即為其單位元。當X為Banach空間時，是Banach代數。