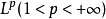線性空間又稱“向量空間”。它是元素(稱為向量)的集，其中有向量的“加法”、數與向量的“乘法”運算，且滿足加法交換律、結合律、分配律，還存在零元素，每個元素有負元素等八條規律。
賦范線性空間是一類可以引進“長度”概念的線性空間。
一致凸賦范線性空間(uniformly convexnormed linear space)是滿足一致凸性的一類賦范線性空間。
基本介紹
- 中文名：一致凸賦范線性空間
- 外文名：uniformly convexnormed linear space
- 領域：數學
- 本質：賦范線性空間
- 性質：一致凸性
- 提出者：克拉克松
- 提出目的：研究拉東-尼科迪姆性質
概念,賦范線性空間,拉東-尼科迪姆性質,巴拿赫空間,巴拿赫代數,
概念
一致凸賦范線性空間(uniformly convexnormed linear space)是滿足一致凸性的一類賦范線性空間。賦范線性空間(X，‖·‖)稱為是一致凸的，如果對任意的ε>0，存在δ>0，使得當‖x‖≤1，‖y‖≤1並且‖x-y‖≥ε時，必有‖x+y‖≥2-δ成立。
是一致凸的。一致凸的巴拿赫空間是自反的。
一致凸空間是巴拿赫空間幾何理論的一個重要概念，它是克拉克松(Clarkson，J.A.)於1936年為研究拉東-尼科迪姆性質而引入的，他開創了從巴拿赫空間的幾何結構出發來研究巴拿赫空間性質的方法。巴拿赫空間的幾何學近年來已成為巴拿赫空間理論研究中人們特別感興趣的一個領域。
賦范線性空間
一類可以引進“長度”概念的線性空間。設X是線性空間，X上滿足下列條件的實值函式p(·)稱為X上的範數：
1.p(x)≥0(x∈X);p(x)=0⇔x=0.
2.p(αx)=|α|p(x)(α為數，x∈X).
3.p(x+y)≤p(x)+p(y)(x，y∈X).
對x∈X，p(x)稱為x的範數，通常記為‖x‖。賦有範數的線性空間(X，‖·‖)稱為賦范線性空間，簡稱賦范空間。
設v是一個線性空間，對v中每個元素a，有一個實數‖a‖與之對應，且具有以下性質：1. ‖a‖≥0，若且唯若a為零時，‖a‖=0; 2.‖ka‖=|k1‖α‖，特別‖-α‖=‖α‖;3.‖α+β‖≤‖α‖+‖β‖，則稱v為賦范線性空間。‖α‖稱為α的範數(模)。
拉東-尼科迪姆性質
拉東-尼科迪姆性質是向量值測度可能具有的一個重要性質，有關問題是理論研究中的重要課題。設(Ω，F，μ)是有限測度空間，X是巴拿赫空間，B(Ω，X，μ)代表定義在Ω上而取值於X的博赫納可積函式全體。如果對每個定義在F上而取值於X的有界變差且關於μ絕對連續的向量值測度E，均存在f∈B(Ω，X，μ)，使得：
E(A)=(B)∫Af(t)dμ (A∈F)，
則說X關於(Ω，F，μ)具有拉東-尼科迪姆性質。如果X關於一切有限測度空間均具有拉東-尼科迪姆性質，則說X具有拉東-尼科迪姆性質。博赫納(Bochner，S.)於1932年提出了如今以他的名字命名的向量值函式的積分——博赫納積分，並且考慮將數值測度論中的拉東-尼科迪姆定理推廣到向量值測度的情況。但是，博赫納發現，對巴拿赫空間L[0，1]，這種推廣是不可行的。因此，需要討論拉東-尼科迪姆定理成立的條件，這樣便產生了巴拿赫空間具有拉東-尼科迪姆性質的概念。伯克霍夫(Birkhoff，G.D.)於1935年證明，希爾伯特空間具有拉東-尼科迪姆性質。克拉克松(Clarkson，J.A.)於1936年引入了一致凸空間的概念，並證明了一致凸巴拿赫空間具有拉東-尼科迪姆性質。蓋爾范德(Гельфанд，И.М.)和莫爾斯(Morse，H.M.)於1936年證明了具有有界完全基的巴拿赫空間具有拉東-尼科迪姆性質。蓋爾豐德(Гелъфонд，А.О.)於1938年證明了自反巴拿赫空間具有拉東-尼科迪姆性質。現在，關於拉東-尼科迪姆性質的研究仍是一個引人注目的課題，並且已經取得了大量的成果。
巴拿赫空間
完備的賦范線性空間被稱為巴拿赫空間，是泛函分析研究的基本內容之一。
20世紀以來，當人們研究了許多具體的無限維空間及其上面相應的收斂性以後，自然而然地轉向抽象形態的線性空間以及按範數收斂的概念。德國數學家希爾伯特、法國數學家弗雷歇和匈牙利數學家裡斯在1904—1918年間所引入的函式空間是建立巴拿赫空間理論的基礎。在這些空間裡，強收斂、弱收斂、緊性、線性泛函、線性運算元等基本概念已經得到初步研究。
1922—1923年，波蘭數學家巴拿赫、奧地利數學家哈恩和美國數學家N.維納等分別獨立地引入了賦范線性空間的概念，並以巴拿赫的姓氏來命名。1922年，巴拿赫開始根據他所引入的公理來系統研究已有的函式空間，得到深刻的結果;同一年，哈恩從當時分析數學的許多成果中提煉出共鳴定理;1922—1923年巴拿赫得到壓縮映射的不動點定理、開映射定理。1927年和1929年哈恩和巴拿赫先後證明了完備賦范空間上泛函延拓定理，引入了賦范線性空間的對偶空間(當時稱之為極空間)，這個定理的推廣形式後來在局部凸拓撲線性空間理論中起了重要作用。1931年，巴拿赫寫成《線性運算元理論》。至此，完備賦范線性空間理論的獨立體系已基本形成，並且在不到十年的時間內便發展成本身相當完整而又有多方面套用的理論。
巴拿赫代數
泛函分析的新分支之一，研究帶有乘法的巴拿赫空間的性質及其套用。
20世紀30年代初，代數環論的重要進展以及它在群表示論上的套用，引起美國數學家馮·諾伊曼的興趣，他於1935年開始研究希爾伯特空間上有界線性運算元的弱閉子環，獲得完整而深入的結果，後人稱這種運算元環為馮·諾伊曼代數。當時也有人進行過關於交換賦范代數的研究，但一直沒有建立起一般理論。
從20世紀30年代末至40年代初，原蘇聯數學家蓋爾范德在定義一般賦范環R後，引進極大理想的概念，建立了R的特徵標空間到R的極大理想空間之間的——對應關係，定義了現被稱為蓋爾范德變換的映射，並證明每個賦范環R都能同態地映射到由R的極大理想構成的豪斯多夫空間上的連續函式環中，等等。他還把此前希爾伯特空間中線性運算元的譜論推廣到賦范代數的元素上，從而建立一般譜論，他定義了R的元素X的譜。為使譜這個概念富有成效，他假定R是完全的，這就是巴拿赫代數。他證明了巴拿赫代數中任一元素X的譜的性質，得到X的譜半徑的優美公式。
蓋爾范德建立的巴拿赫代數理論，幾十年來一直是泛函分析最活躍的研究領域之一。它不僅成為研究局部緊群理論的重要工具，而且在研究經典分析的某些課題中也取得了重要成果。
