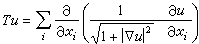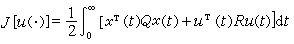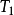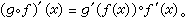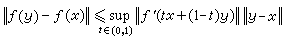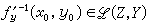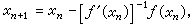概念,常見的非線性積分運算元,烏雷松運算元,沃爾泰拉運算元,哈默斯坦運算元,常見的微分運算元,KdV運算元,極小曲面運算元,蒙日-安培運算元,概念,運算元的微分學,運算元的微分學與函式的微分學相似地方,不動點及可解性,壓縮型運算元,單調運算元,緊運算元,半序結構,非線性特徵值問題,
概念
人們從兩種不同的途徑研究非線性問題:①針對具體問題,考察具體非線性運算元的特徵,解釋非線性現象。②從一般的運算元概念出發,添加適當的分析、拓撲或代數性質導出一些一般性的結論。
代數、幾何、拓撲中各種非線性映射是形形色色的,分析學中經常遇到的非線性運算元則大抵由乘法、函式的複合以及各種線性運算元組合而成。
運算元高階導數的概念要求引入多線性運算元,實際上,高階 F導數還是對稱的多線性運算元。帶餘項的泰勒公式在形式上與函式的泰勒公式是一樣的。
積分學也被推廣到一般運算元。黎曼積分的定義與普通函式的積分定義一樣,而勒貝格積分的推廣則分強、弱兩種,前者稱為博赫納積分,後者稱為佩蒂斯積分(見向量值積分)。
常見的非線性積分運算元
烏雷松運算元
.其中
K(
x,
y,
t)是 0≤
x,
y≤1,
t∈
R上的連續函式

沃爾泰拉運算元
哈默斯坦運算元
*其中
K 是【0,1】×【0,1】上某
p次可積函式,
ƒ(
y,
t)在【0,1】×
R上可測,對固定的
y關於
t連續。


常見的微分運算元
KdV運算元
極小曲面運算元
蒙日-安培運算元
概念
許多非線性運算元出現於非線性方程之中,從而有關非線性運算元的理論就圍繞著非線性方程的求解的研究而展開。設T是從B空間(巴拿赫空間)X到B 空間Y的運算元,設y∈Y,求解x∈X,滿足:
(1)
有時特別地考察
y=
θ(
θ是
Y 中的零元)的情形,稱解
x為
T的零點。顯然,若
T是一個滿射,則(1)總有解,於是人們討論在什麼條件下
T具有滿射性.又若
X=
Y,方程(1)的求解問題有時化歸尋求運算元
x =
Tx+
x-
y的不動點
(2)的問題。這樣提問題有助於利用幾何直觀。

和線性方程的解集總是仿射集(線性子空間的平移)不同,方程(1)的解集構造很複雜,它可能對某些y是空集,而對另一些y則非空。其個數可能只有一個,可能有有窮多個,也可能有無窮多個;可能是孤立的,可能有聚點,也可能是連續統。
以X為定義域,取值為Y(映X入Y中)的子集的映射,稱為集值映射。相應於(1)的求解問題寫成下列從屬關係:
運算元的微分學
從分析上研究一般運算元的途徑是把數學分析中研究函式的微積分學推廣到運算元。設
X、
Y都是
B空間,
U是
X中的一個開集,
ƒ:
U→
Y,稱
ƒ在
連續,是指。相應於方嚮導數概念的是加托導數,簡作
G導數。稱
ƒ在
處
G可微,是指對任意的
h∈
X,存在d
ƒ(
,
h∈
Y,使得,


當
t→0,
+
th∈
U。稱d
ƒ(
,
h)為
ƒ在
處沿方向
h的
G導數。相應於全微分概念的是弗雷歇導數,簡作
F導數。稱
ƒ在
處
F可微,是指存在
A∈
L(
X,
Y),(
L(
X,
Y)表示
X到
Y的線性有界運算元空間)
X→
Y是線性有界運算元空間,使得對任意的
h∈
X,當
+
h∈
U時,有

當
h→
θ。稱
A為
ƒ在
處的
F導數,並且記作
ƒ┡(
)。
G可微與
F可微之間的關係如下:①若
ƒ:
U→
Y在
處
F可微,則
ƒ在
必
G可微,並且,任意的
h∈
X。②設
ƒ:
U→
Y 在
U 內
G可微,且d
ƒ(
x,
h)關於
h線性,即d
ƒ(
x,·∈
L(
X,
Y),任意的
x∈
U。如果d
ƒ(
x,·)還是關於
x連續的,那么
ƒ在
x∈
U是
F 可微的。

運算元的微分學與函式的微分學相似地方
運算元的微分學與函式的微分學很相似。
① 鎖鏈法則 設
X、
Y、
Z、是
B空間,
U嶅
X,
V嶅
Y是開集。若
ƒ:
U→
Y F可微;
g:
V→
Z F可微;且
ƒ(
U)嶅
V,則
g。
ƒ在
U內
F可微,並且
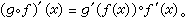
② 中值不等式 設 ƒ:U →Y F 可微,又設線段
則。
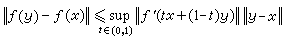
③ 反函式定理 設
ƒ:
U→
Y在
U上有連續的
F 導數
ƒ┡(
x),又若式中
,則
ƒ是0的一個鄰域到
ƒ(
)的一個鄰域的微分同胚,並且


④ 隱函式定理 設
X、
Y、
Z 是
B 空間,
O 是
X×
Y中的一個開集,(
x0,
y0∈
O,又設
ƒ:
O→
Z連續,滿足:
,
ƒ在
O上關於
y的
F導數
ƒ┡(
x,
y)是連續的,並且,則必存在
的一個鄰域
U和
y0的一個鄰域
V,以及惟一的連續映射
φ:
U→
V,滿足
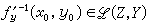

隱函式定理與反函式定理對於求解運算元方程 (1)有十分重要的意義。它們表明:對於具有連續導數的一般非線性運算元,只要在一點上,它的線性化方程是可解的(在一定意義下),那么它在這點附近便是可解的。許多非線性方程的局部可解性理論都基於這一基本事實。
為了近似求解方程,
ƒ(
x)=
θ,數學分析里的牛頓求根法,也被推廣。在準確解
x∈
U的鄰近任取
,構作疊代序列:
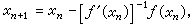
然而,反函式定理有時不夠用,其中
的條件不滿足。這種情形在一些微分方程理論中出現,例如,線性運算元
ƒ┡(
)不能保持值域中的函式足夠光滑。為此,J.K.莫澤修改了牛頓求根法的疊代格式,並用它來推廣反函式定理。由此發展起來的一套技巧在好幾個重要的問題中非常有效。例如小除數問題、黎曼流形的嵌入問題等,被稱之為納什-莫澤技巧。

反函式定理給出了 ƒ成為局部同胚的條件。為了得到整體性的同胚,僅用微分學是不夠的,藉助於緊性概念以及拓撲學中的同倫概念可以得到整體的反函式定理:為了使連續映射ƒ是一個同胚,必須且僅須它是局部同胚,並有ƒ是固有的。所謂運算元ƒ是固有的,指緊集的原像是緊集。
Y=
R或
C的映射稱為泛函,設
φ:
U→
R,
x0∈
U稱為它的一個局部極小 (或極大)點,如果
φ(
x)≥
φ(
)(或
φ(
x)≤
φ(
)對一切
x∈
V,其中
V是
的某個鄰域。費馬原理被自然地推廣:設
φ在
達到局部極值,且
φ在
處
G可微,則d
φ(
,
h)=
θ,對任意的
h∈
X。在變分學中,它對應著泛函極值的必要條件即歐拉方程。
一般地,稱
φ┡(
)=
θ的點
x0為泛函
φ的臨界點。一個運算元
T:
X→
X(
X表示
X的共軛空間),稱為位運算元,如果存在
φ:
X→
R,使得
Tx=
φ┡(
x)。因此,對於位運算元,求解問題(1)便化歸求泛函
φ的臨界點(見
變分法、
大範圍變分法)。
不動點及可解性
下面是幾類重要的不動點定理。
壓縮型運算元
一個最簡單、熟知、套用最廣泛的不動點定理是壓縮映射定理。在一個度量空間(
X,
d)上,
T映
X至自身,稱其為壓縮的,如果
d(
Tx,
Ty)≤
αd(
x,
y)對任意的
x,
y∈
X,式中0<
α<1。每個壓縮運算元在
X中必有唯一的不動點。這個不動點可以從任意點
出發,通過簡單疊代法求出。令,
n=1,2,…,則
Xn收斂到不動點。條件
α<1一般不能去掉。在定義中若
α=1,則稱
T為非擴張運算元。實直線上的一個平移顯然是非擴張的,但沒有不動點。然而對於一致凸的
B空間的一個閉、凸、有界子集
C,若
T:
C→
C是非擴張的,則
T在
C上必有不動點。對於壓縮運算元的研究導致下列逆問題:若
T:
X→
X,則在什麼條件下能在
X中引入可度量化的拓撲,使得
T是一個壓縮運算元。答案是:每個
T,
n=1,2,…,在
X中都只有惟一的不動點。
單調運算元
單調運算元的概念起源於可微凸泛函的導數。設φ是在B 空間X 上定義的這種函式,則〈φ┡(x)-φ┡(y),x-y〉≥0,對任意的x,y∈X,其中<,>表示X與X 之間的對偶。直線上的可微凸函式的導函式是單調不減的,於是就把滿足下面這些條件的運算元T:X→X,
稱為單調運算元,如果α>0則稱為強單調運算元。自反B空間上弱線段連續的強單調運算元是 X→X 的滿射(所謂弱線段連續,指對任意的x,y∈X,T(x+ty)→T(x)當 t→0)。這個滿射性定理是G.J.明蒂、F.E.布勞德給出的,它在非線性運算元半群理論、非線性發展方程以及一類非線性橢圓型方程的存在性理論中經常用到。
緊運算元
在從有窮維到無窮維空間的過渡中,運算元的緊性概念起重要的作用。所謂T是緊運算元,是指它連續,並映有界閉集入緊集。利用緊性,J.P.紹德爾把布勞威爾不動點定理推廣到賦范線性空間:任意一個映非空、有界、閉、凸集C於自身的緊運算元至少在C上有一個不動點。這個定理是一個非常基本的不動點定理。尤其在微分方程理論中,它是證明存在性的一個重要依據。
紹德爾不動點定理的另一種形式是把運算元的緊性減弱為連續性,而集合
C則加強要求是緊的。從幾何上看,這種形式的不動點的存在問題可以化歸更一般的一族集合具有非空交的問題:對任意
x∈
C,令
G(
x)={
y∈
C|‖
y-
Ty‖≤‖
x-
Ty‖}。顯然,若有
∈∩{
G(
x)|
x∈
C},則
是
T的不動點。樊畿在一般拓撲線性空間的子集
A上考察到這空間的集值映射
F。他證明:設
F滿足對任意的有窮子集,又設
F(
x)是閉子集,並且其中至少有一個是緊的,則∩{
F(
x)|
x∈
A}≠═。從這定理導出的一系列不動點定理和相交性定理在
對策論與數理經濟學中占據重要的位置。
有窮維空間之間的連續映射的拓撲度常被用來估計不動點的個數,它也是證明各種不動點定理的有力工具。J.勒雷、紹德爾將這一概念推廣到B 空間上的恆同運算元的緊擾動T=Id-K其中K是緊運算元。對於有界開集Ω,當p唘T(дΩ)時,記degLS(T,Ω,p)為對應的勒雷-紹德爾度,它具有下列基本性質。①同倫不變性:設Kt在捙×【0,1】上緊,Tt=Id-Kt,當p唘Tt(дΩ)對任意的t∈【0,1】時,則degLS(Tt,Ω,p)=常數。②平移不變性:degLS(T,Ω,p)=degLS(T-p,Ω,θ)。③區域可加性:設開集Ω1,Ω2嶅Ω滿足:且,則④規範性:
涉及到緊性的勒雷-紹德爾度以及由其導出的不動點定理可以推廣到一些非緊運算元類。由K.庫拉托夫斯基的非緊性度量概念規定的一些運算元類,例如,α集壓縮運算元,它包含緊運算元為特殊情形,就屬這種非緊運算元類。此外,對非線性弗雷德霍姆運算元也能定義拓撲度,使之保持許多重要性質。後者在無窮維流形的研究中經常要用到。
在另一個方向上,勒雷-紹德爾度和有關的不動點定理還被推廣到集值映射F,其中F(x)是凸集。
半序結構
在關序空間(P,≤)上,一個運算元T:P→P稱為是保序的,如果x≤y蘊含了Tx≤Ty對任意的x,y∈P。對保序運算元也有許多不動點定理,類似於壓縮映射定理,在半序結構中有如下結論:若存在b∈P使得b≤Tb,且P的每個全序子集都有上確界,則T的不動點集非空,且有極大元。這種類型的不動點定理在代數學、自動機理論以及計算方法中很有用。
即使在完備度量空間(X,d)上,本來沒有半序結構,但可藉助於一個實值函式 φ來規定半序。下列不動點定理甚至對運算元T沒有連續要求。設T:X→X是任一映射,滿足:d(x,Tx)≤φ(x)-φ(Tx),對任意x∈X,式中φ是下半連續的、有下界的實值函式,則T至少有一個不動點。
非線性特徵值問題
求解帶參數
λ的非線性運算元方程 (4)

的非零解問題稱為非線性特徵值問題。這裡當然是假定了T(θ,λ)呏θ。對應的λ稱為非線性特徵值,而解 x≠θ則稱為特徵元。
線性運算元方程的特徵集合是線性子空間,但一般的非線性運算元方程的非零解集={(x,λ)|T(x,λ)=θ,x≠θ}的構造卻非常複雜。
先在局部範圍考察集合。因為(θ,λ)都是(4)的解,所以我們把(θ,λ0)稱為方程(4)的分歧點,如果在它的任意一個鄰域內都有(4)的非零解。按隱函式定理,可知只要在λ=λ0處的線性化運算元Tx(θ,λ0)是非奇異的,並有有界逆,就能斷定在(θ,λ0)的一個鄰域內(4)沒有非零解,即 (θ,λ0)不是分歧點。但即使Tx(θ,λ0)奇異,(θ,λ0)可以是分歧點,也可以不是分歧點。即使是分歧點,在這點附近的解集構造也可能是各種各樣的:可以是一列以 (θ,λ0)為聚點的點集,可以是一條連續曲線,也可以是若干條不同的曲線或曲面,如圖(縱坐標表示‖x‖)所示。
當T(·,λ0)是弗雷德霍姆運算元時,在(θ, λ0)點附近的行為可以通過一種約化手續化歸有窮維方程的研究。至於的整體行為知道得不多,常用拓撲方法去討論。
希爾伯特空間上緊、位運算元的特徵值問題可以仿照線性緊、自伴運算元的譜理論,通過泛函的極值來研究。當A是線性緊自伴運算元時,二次函式在單位球面上的臨界點就是A的特徵元,而特徵值是作為拉格朗日乘子出現的。類比於此,當A是某個弱連續泛函φ的導運算元時,又若Ax≠θ對任意的x≠θ,則存在с≠φ(θ),使得流形,模平方函式‖x‖在M 0上達到極小值點。這個極小值點就是A的特徵元,而對應的拉格朗日乘子則是非線性特徵值的倒數。φ 還是偶泛函時,利用極小極大原理可以獲得更多的臨界值點。