烏雷松非線性積分運算元

烏雷松非線性積分運算元是一類相當廣泛的非線性積分運算元。這類運算元是由烏雷松於1924年首先提出並加以研究的。

基本介紹

• 中文名：烏雷松非線性積分運算元
• 外文名：Urysohn nonlinearintegral operator
• 適用範圍：數理科學

簡介

烏雷松非線性積分運算元是一類相當廣泛的非線性積分運算元。

設k(x,y,u):G×G×R¹→R¹是可測函式，則形如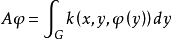

的運算元稱為烏雷松非線性積分運算元。

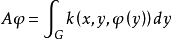
性質

全連續性是非線性積分運算元的重要性質。

如果k(x,y,u)在G×G×R¹上連續，則烏雷松非線性積分運算元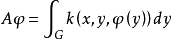是作用在C(G)上的全連續運算元。

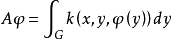
進一步，下列結果成立：若G是具有非零測度的有界閉集，對一切x∈G，和幾乎一切y∈G，k(x,y,u)關於u連續，並且對一切x∈G，u∈R¹，k(x,y,u)關於y可測，則相應的烏雷松非線性積分運算元映C(G)入自身全連續的充分必要條件是，對任給a>0，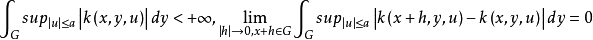

對一切x∈G成立。

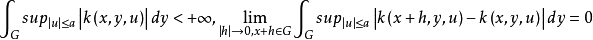
發展

烏雷松非線性積分運算元是一類很廣泛的運算元類，包含了哈默斯坦非線性積分運算元和沃爾泰拉非線性積分運算元作為特殊情況。這類運算元由於過於廣泛，研究起來困難很大，所以到目前為止，除了在該類運算元的全連續判別上有了較系統的結果之外，關於烏雷松非線性積分方程解的性質的研究，結果是很少的，還有待於人們去探索。

這類運算元是由烏雷松於1924年首先提出並加以研究的。