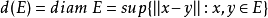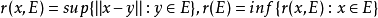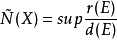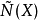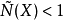正規結構(normal structure)是關於有界閉凸子集的點到該集的其他點的距離與該集的直徑之間關係的一個概念。設A是巴拿赫空間X的有界閉凸集，x∈A，若sup{‖x-y‖|y∈A}<diamA，則x稱為A的非直徑點。設V為巴拿赫空間X的子集，若V的每個有界閉凸子集都具有非直徑點，則稱V具有正規結構。
基本介紹
- 中文名：正規結構
- 外文名：normal structure
- 領域：數學
- 意義：有界閉凸子集的點與直徑關係
- 場合：巴拿赫空間
- 套用：非擴張映射的不動點存在性
概念,巴拿赫空間,不動點定理,套用,
概念
正規結構(normal structure)是關於有界閉凸子集的點到該集的其他點的距離與該集的直徑之間關係的一個概念。設A是巴拿赫空間X的有界閉凸集，x∈A，若sup{‖x-y‖|y∈A}<diamA，則x稱為A的非直徑點。設V為巴拿赫空間X的子集，若V的每個有界閉凸子集都具有非直徑點，則稱V具有正規結構。正規結構的概念在巴拿赫空間結構理論和非擴張映射的不動點存在性中均有套用。
巴拿赫空間
按範數導出的距離完備的賦范線性空間.設(X，‖·‖)為賦范線性空間。對x，y∈X，ρ(x，y)=‖x-y‖定義了X上的一個距離，使X成為度量空間。如果X按這個距離是完備的，就稱X為巴拿赫空間。L(Ω)(1≤p≤+∞)，C(Ω)，c，c0等都是巴拿赫空間的例子。
巴拿赫空間(含賦范空間)是1922年巴拿赫(Banach，S.)與維納(Wiener，N.)相互獨立提出的，並且在不到10年的時間內便發展為相當完美而又有多方面套用的理論。1932年，巴拿赫論述這部分理論的《線性運算元理論》一書的問世，是泛函分析作為獨立的數學分支出現的標誌。巴拿赫空間至今仍是泛函分析研究的基本對象之一。
完備的賦范線性空間被稱為巴拿赫空間，是泛函分析研究的基本內容之一。
20世紀以來，當人們研究了許多具體的無限維空間及其上面相應的收斂性以後，自然而然地轉向抽象形態的線性空間以及按範數收斂的概念。德國數學家希爾伯特、法國數學家弗雷歇和匈牙利數學家裡斯在1904—1918年間所引入的函式空間是建立巴拿赫空間理論的基礎。在這些空間裡，強收斂、弱收斂、緊性、線性泛函、線性運算元等基本概念已經得到初步研究。
1922—1923年，波蘭數學家巴拿赫、奧地利數學家哈恩和美國數學家N.維納等分別獨立地引入了賦范線性空間的概念，並以巴拿赫的姓氏來命名。1922年，巴拿赫開始根據他所引入的公理來系統研究已有的函式空間，得到深刻的結果；同一年，哈恩從當時分析數學的許多成果中提煉出共鳴定理；1922—1923年巴拿赫得到壓縮映射的不動點定理、開映射定理。1927年和1929年哈恩和巴拿赫先後證明了完備賦范空間上泛函延拓定理，引入了賦范線性空間的對偶空間(當時稱之為極空間)，這個定理的推廣形式後來在局部凸拓撲線性空間理論中起了重要作用。1931年，巴拿赫寫成《線性運算元理論》。至此，完備賦范線性空間理論的獨立體系已基本形成，並且在不到十年的時間內便發展成本身相當完整而又有多方面套用的理論。
不動點定理
亦稱尼爾森不動點理論或稱拓撲不動點理論，是代數拓撲學的一個經典研究方向。對於一個自映射f：X→X，集合X中滿足條件f(x)=x的點稱為映射f的不動點。該理論就是研究拓撲空間中自映不動點集的特徵，它是各種方程解的存在性等問題的抽象化。
該理論問題的研究開始於尼爾森(Nielsen，J.)關於環面上自同胚的不動點個數問題，這一方法被賴德邁斯特(Reidemeister，K.W.F.)等人推廣至緊多面體的任意連續映射，相應的不變數被稱為尼爾森數.一個映射的尼爾森數是它所在的映射同倫類中所有映射不動點個數的下界。
另一個拓撲不變數是萊夫謝茨數，一個映射的萊夫謝茨數非零決定了該映射必存在不動點。
不動點類理論的進一步研究問題有：尼爾森數、萊夫謝茨數與其他拓撲不變數的關係，它們的理論計算問題，各種特殊類型的空間及映射的不動點集特徵問題等。另外，這一理論中的方法亦被用來研究映射的周期點問題。
中國數學家在這一領域中有很好的研究工作。姜伯駒解決了一類拓撲空間(被稱為姜空間)中自映射的尼爾森數的計算問題，並首先給出了萊夫謝茨數為零但尼爾森數非零的映射的例子，這說明了在判別不動點存在的問題上，後一個不變數要優於前一個不變數。
套用
設E是Banach空間X的非空有界凸閉子集，記
為E的直徑。對x∈E，記
。正規結構係數為：
，注意到，MALUTA定義的正規結構係數
是BYNUM定義的N(x)的倒數。如果
，則稱空間X具一致正規結構。而具一致正規結構的空間是自反空間，一致凸和一致光滑的Banach空間均具一致正規結構。
