正規化方均根差

正規化方均根差（Normalized root mean square error）是將方均根差化正規化後所得的統計數值，其正規化的方法有很多種。

基本介紹

• 中文名：正規化方均根差
• 外文名：Normalized root mean square error
• 定義：將方均根差化正規化
• 領域：數學

簡介

正規化方均根差（Normalized root mean square error）是將方均根差化正規化後所得的統計數值。

定義

在影像處理中，給定兩個影像矩陣 x[m,n]和 y[m,n]，其正規化方均根差可被定義如下：

此數值常被用來作為測量訊號之間結構相似度(Structural Similarity)的評估工具。這個值常被用來指正規化的方均根偏移或誤差，同時也常常被表示成比例。當比例的值較低時，代表較少的殘差變異。在很多情況下，特別是取較小的樣本的時候，樣本的範圍容易被樣本的大小影響，其準確度可能就受到影響。

當以平均值來正規化量測值時，均方根差的變異係數可能被用來避免混淆。這和均方根差在標準差上的變異係數是相同的。

結構相似度

為此，影像學家們提出了一種新的計算結構相似度的概念，其式子如下：

為x,y的平均數。

為x,y的變異數。

為x,y之間的共變異數。

為可調整的常數。

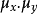
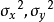
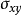
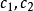
L為信號x的最大可能值減去最小可能值。

均方根誤差

均方根誤差（或稱方均根偏移、均方根差、方均根差等，英文：root-mean-square deviation、root-mean-square error、RMSD、RMSE）是一種常用的測量數值之間差異的量度，其數值常為模型預測的量或是被觀察到的估計量。方均根偏移代表預測的值和觀察到的值之差的樣本標準差（sample standard deviation），當這些差值是以資料樣本來估計時，他們通常被稱為殘差；當這些差值不以樣本來計算時，通常被稱為預測誤差（prediction errors）。方均根偏移主要用來聚集預測裡頭誤差的大小，通常是在不同的時間下，以一個量值來表現其預測的能力。方均根偏移是一個好的準度的量度，但因其與數值範圍有關，因此被限制只能用來比較不同模型間某個特定變數的預知誤差。

缺點

然而，正規化方均根差在理論上雖然是合理的架構，但實際上可能無法完全反映出人眼所見影像的相似度。

也就是說，在肉眼上，我們認為的相近，但要是用NRMSE來評估，其會認為左圖和中圖是較為接近的，因此NRMSE並不符合人眼所見影像的相似度。

套用

其正規化的方法有很多種。

• 在信號處理中，我們會以其訊號強度來正規化方均差。
  
• 在氣象學上，可用來評估一個數值模型可以多好的預測大氣層的行為。
  
• 在生物資訊學中，均方根差被用來量測重疊蛋白質（superimposed proteins）分子間的距離。
  
• 在結構藥物設計中，均方根差被用來測量配體（ligand）的晶格構造以及對接預測（docking prediction）。
  
• 在經濟學中，均方根差被用來覺得一個模型是否符合經濟指標。部分專家曾提出均方根差比相對絕對誤差（relative absolute error）來的不可靠。
  
• 在實驗心理學中，分均根差被用來指示一個數學或計算行為模型（mathematical or computational models）能解釋實際觀察行為的良好程度。
  
• 在地理資訊系統中（GIS），均方根差是一種用來量測空間分析和遠距偵測的量度。
  
• 在水文地質學中，均方根差和正規化均方根差被用來評估地下水模型的刻度。
  
• 在影像科學中，均方根差是一種峰值訊噪比，是一種用來檢視一個方法能多好的去重建原來的影像。
  
• 在計算神經科學中，均方根差被用來檢視一個系統能學習一個給定模型的能力。
  
• 在蛋白質核磁共振光譜學中，均方根差被用來當作一個評估結構品質的量度。