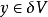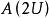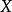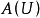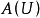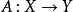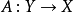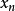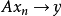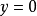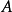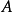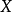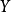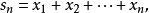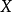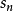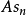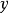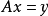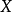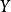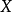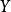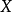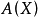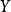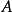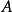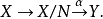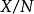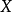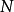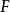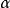結果
開映射定理有一些重要的結果:
1.如果
是巴拿赫空間
X和
Y之間的
雙射連續線性運算元,那么逆運算元
也是連續的。(Rudin 1973, 推論2.12) ;
2.如果
是巴拿赫空間
X和
Y之間的
線性運算元,且如果對於
X內的每一個
序列(
),只要
xn → 0且
就有
,那么
A就是連續的(
閉圖像定理)。(Rudin 1973, 定理2.15)。
證明
我們需要證明,如果
是
巴拿赫空間之間的連續線性滿射,那么
就是一個開映射。為此,只需證明
把
內的單位球映射到
的原點的一個鄰域。
設
分別為
和
內的單位球。那么
是單位球的倍數
的序列的交集,
,且由於
是滿射,
根據
貝爾綱定理,巴拿赫空間
不能是可數個
無處稠密集的並集,故存在
,使得
的
閉包具有非空的
內部。因此,存在一個開球
,其中心為
,半徑
,包含在
的閉包內。如果
,那么
和
位於
內,因此是
的
極限點,根據加法的連續性,它們的差
是
的極限點。根據
A的線性,這意味著任何
都位於
的閉包內,其中
。於是可以推出,對於任何
和任何
,都存在某個
,滿足:
固定
。根據(!),存在某個
,滿足
且
||
y−
A x 1||<
δ / 2。定義序列
如下。假設:
設
從(2)的第一個不等式可知,
是一個
柯西序列,且由於
是完備的,
收斂於某個
。根據(2),序列
趨於
,因此根據
A的連續性,有
。而且:
這表明每一個
都屬於
,或等價地,
內的單位球的像
包含了
Y內的開球
。因此,
是
內0的鄰域,定理得證。
推廣
或
的局部凸性不是十分重要的,但完備性則是:當
和
是F空間時,定理仍然成立。更進一步,這個定理可以用以下的方法與
貝爾綱定理結合(Rudin, 定理2.11):
設
為F空間,
為
拓撲向量空間。如果
是一個連續線性運算元,那么要么
是
內的貧集,要么
。在後一個情況中,
是開映射,
也是
空間。 更進一步,在這個情況中,如果
是
的
核,那么
有一個標準分解,形如下式:
其中
是
對
閉子空間
的
商空間(也是
空間)。商映射
是開放的,且映射
是
拓撲向量空間的
同構(Dieudonné, 12.16.8)。
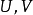 分別為
分別為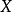 和
和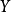 內的單位球。那么
內的單位球。那么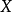 是單位球的倍數
是單位球的倍數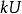 的序列的交集,
的序列的交集,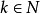 ,且由於
,且由於 是滿射,
是滿射,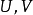
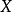
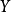
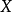
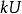
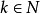

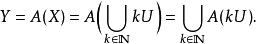
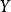 不能是可數個無處稠密集的並集,故存在
不能是可數個無處稠密集的並集,故存在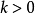 ,使得
,使得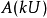 的閉包具有非空的內部。因此,存在一個開球
的閉包具有非空的內部。因此,存在一個開球 ,其中心為
,其中心為 ,半徑
,半徑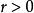 ,包含在
,包含在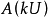 的閉包內。如果
的閉包內。如果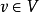 ,那么
,那么 和
和 位於
位於 內,因此是
內,因此是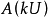 的極限點,根據加法的連續性,它們的差
的極限點,根據加法的連續性,它們的差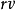 是
是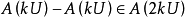 的極限點。根據A的線性,這意味著任何
的極限點。根據A的線性,這意味著任何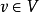 都位於
都位於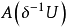 的閉包內,其中
的閉包內,其中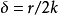 。於是可以推出,對於任何
。於是可以推出,對於任何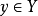 和任何
和任何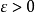 ,都存在某個
,都存在某個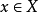 ,滿足:
,滿足: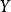
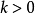
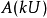


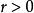
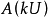
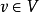



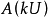
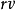
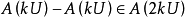
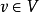
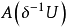
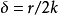
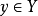
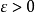
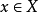

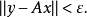
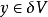 。根據(!),存在某個
。根據(!),存在某個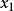 ,滿足
,滿足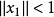 且
且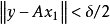 ||y−A x 1||<δ / 2。定義序列
||y−A x 1||<δ / 2。定義序列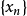 如下。假設:
如下。假設: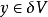
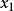
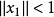
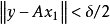
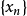

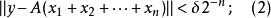
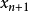 ,使得:
,使得: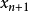
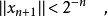
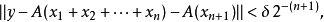
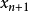
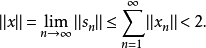
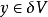 都屬於
都屬於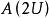 ,或等價地,
,或等價地,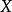 內的單位球的像
內的單位球的像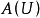 包含了Y內的開球
包含了Y內的開球 。因此,
。因此,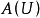 是
是 內0的鄰域,定理得證。
內0的鄰域,定理得證。