基本介紹
- 中文名:商空間
- 外文名:quotient space
- 領域:數學
- 性質:反身性,對稱性,傳遞性
- 公式:V/N
定義









性質




性質推廣






















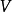






商空間
定義
例子







































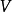










線上性代數中,一個向量空間V被一個子空間N的商是將N“坍塌”為零得到的向量空間,所得的空間稱為商空間(quotient space),記作V/N(讀作V模N)。...
《商空間與粒計算:結構化問題求解理論與方法》是2010年6月1日科學出版社出版的圖書。本書通過豐富的文獻資料和研究工作,對結構化問題求解的粒計算研究的已有成果及...
商度量空間是度量空間的一種,一個拓撲空間是序列的,若且唯若該空間是個度量空間的商空間。...
《商空間與粒計算——結構化問題求解理論與方法》是2010年科學出版社出版的圖書,作者是張燕平、羅斌、姚一豫、苗奪謙、王國胤、張鈴、張鈸。...
在數學中,Lp空間是由p次可積函式組成的空間;對應的ℓp空間是由p次可和序列組成的空間。它們有時叫做勒貝格空間,以昂利·勒貝格命名,儘管依據Bourbaki (1987)...
基本信息基於商空間的問題求解(Quotient Space Based Problem Solving) 作者:張鈴、張鈸 ISBN:9787302384953 定價:120元 印次:1-1 裝幀:精裝 印刷日期:2014-12-8...
軌道空間(orbit space)是一類特殊的商空間,若G是拓撲群,X是拓撲空間,G中每一元素g誘導一個從X到自身的同胚映射,x↦g(x),其中x∈X,對於任意g,h∈G,滿足...
《問題求解理論及套用:商空間粒度計算理論及套用》是2007年3月1日清華大學出版社出版的圖書,作者是張鈴、張鈸。...
拓撲線性空間是泛函分析的重要分支,又稱之為拓撲向量空間,它是具有拓撲結構的線性空間,是賦范線性空間概念的推廣。局部凸空間是最重要的一類拓撲線性空間。設E是...
核型空間(nuclear space)是一類局部凸空間。局部凸空間是最重要的一類拓撲線性空間。設E是拓撲線性空間,如果E中存在由均衡凸集組成的零元的鄰域基,就稱E是局部凸...
在數學領域拓撲學中,一致空間是帶有一致結構的集合。一致空間是帶有用來定義一致性質如完備性、一致連續和一致收斂的附加結構的拓撲空間。一致空間的概念是韋伊(Weil,...
商賦范線性空間是由賦范線性空間與其閉子空間誘導出的新的賦范線性空間。...... 商賦范線性空間是由賦范線性空間與其閉子空間誘導出的新的賦范線性空間。...
在拓撲學和相關的數學領域中,吉洪諾夫空間或完全正則空間是特定優良種類的拓撲空間。這些條件是分離公理的個例。吉洪諾夫空間得名於安德列·尼古拉耶維奇·吉洪諾夫(...
在數學中, Lp空間是由p次可積函式組成的空間;對應的lp空間是由 p次可和序列組成的空間。在泛函分析和拓撲向量空間中,他們構成了Banach空間一類重要的例子。...
在拓撲結構和相關的數學領域,斯通空間是一個非空的緊湊型完全不連線的豪斯多夫空間。這樣的空間也被稱為無限空間。他們以馬歇爾·哈維·斯通(Marshall Harvey Stone)...
布爾空間(Boolean space)是一種特殊的拓撲空間。拓撲空間是歐幾里得空間的一種推廣。給定任意一個集,在它的每一個點賦予一種確定的鄰域結構便構成一個拓撲空間。...
作者:(日)兒玉之宏,(日)永見啟應著,方嘉琳 譯。本書是點集拓撲學方面的一本經典著作,全書共十章,內容為:拓撲空間、積空間、仿緊空間、緊空間、一致空間、...
數學中,一個辛向量空間是帶有辛形式ω 的向量空間 V,所謂辛形式即一個非退化斜對稱的雙線性形式。...
張鈸在學術研究上的主要貢獻是提出問題分層求解的商空間理論,通過代數的方法,系統地解決了不同層次求解空間的問題表達、複雜性分析、不同層次空間之間信息、運算元及...
