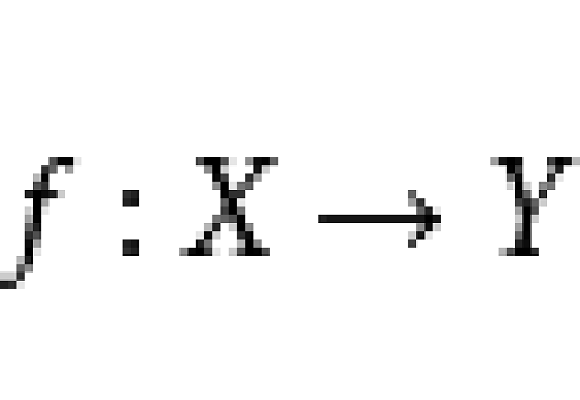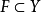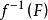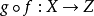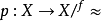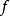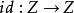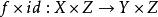基本介紹
- 中文名:商映射
- 外文名:quotient mapping
- 所屬學科:數學
- 性質:一種連續映射
定義,相關定理,常用命題,舉例,
定義
實際上容易看出,商映射即是滿足下列兩個(等價的)條件之一的滿映射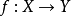
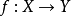
(1)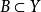 是開集
是開集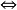
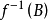 是X的開集;
是X的開集;
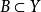
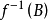
相關定理
證明: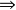 :顯然成立。
:顯然成立。
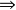
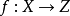
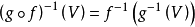
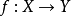
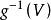
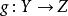
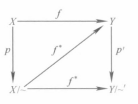
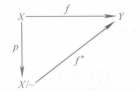 圖一
圖一(1)存在唯一的映射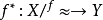 使得
使得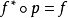 ,且
,且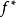 是單射,即圖一可交換,
是單射,即圖一可交換,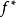 叫
叫 的誘導映射;
的誘導映射;
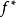
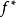

(3)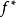 連續
連續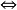
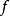 連續。
連續。
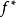
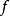
定理2 沒X,Y是兩個拓撲空間,~和~’分別為X和Y上的等價關係,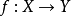 是一個連續映射,且保持關係,即
是一個連續映射,且保持關係,即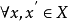 ,
,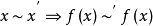 ,則存在一個連續映射
,則存在一個連續映射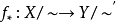 使得圖二是個交換圖(其中
使得圖二是個交換圖(其中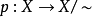 和
和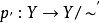 均表示自然映射),並且當
均表示自然映射),並且當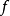 是商映射時,
是商映射時,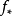 也是商映射。
也是商映射。
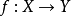
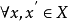
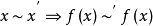
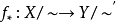
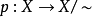
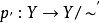
 圖二
圖二定理4 設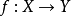 是商映射,並且X是局部連通的,則Y也是局部連通的。
是商映射,並且X是局部連通的,則Y也是局部連通的。
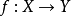
常用命題
關於商映射,有如下一些基本而常用的命題。
命題1 開的(或閉的)連續滿映射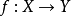 是商映射。
是商映射。
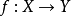
但是這個命題的逆命題並不成立。
命題2 如果X是緊緻的,Y是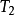 空間,則連續滿映射
空間,則連續滿映射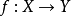 是商映射。
是商映射。
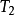
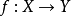
證明 只需證明f是閉映射即可,對於x中任一閉子集F,由於X是緊空間,故F是緊子集,從而f(F)是Y的緊子集,由於Y是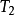 空間,故f(F)是閉的,因此f是閉映射。
空間,故f(F)是閉的,因此f是閉映射。
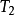
命題3 商映射的複合映射仍然是商映射。
命題4 若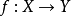 是商映射.則商空間
是商映射.則商空間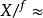 與Y同胚。
與Y同胚。
舉例
例1 在由正方形粘出圓柱面,環面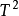 ,
,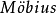 帶,Klein瓶及射影平面的例子中,對應的粘合映射就是相應的商映射。
帶,Klein瓶及射影平面的例子中,對應的粘合映射就是相應的商映射。
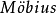
例2 將三角形兩邊同向地粘接得到什麼空問?
通過圖三,四可以看出,適當改變粘合順序,我們可知所得也是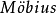 帶:先沿b剪開,再粘合a,最後粘合b,即得到
帶:先沿b剪開,再粘合a,最後粘合b,即得到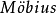 帶。
帶。
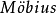
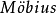
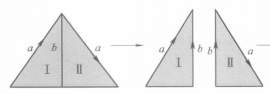 圖三
圖三 圖四
圖四