商賦范線性空間是由賦范線性空間與其閉子空間誘導出的新的賦范線性空間。
基本介紹
- 中文名:商賦范線性空間
- 外文名:quotiently normed linearspace
- 適用範圍:數理科學
簡介

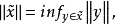
性質
賦范線性空間







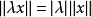



商賦范線性空間是由賦范線性空間與其閉子空間誘導出的新的賦范線性空間。

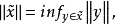







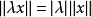



商賦范線性空間是由賦范線性空間與其閉子空間誘導出的新的賦范線性空間。...... 商賦范線性空間是由賦范線性空間與其閉子空間誘導出的新的賦范線性空間。...
賦準范線性空間(paranormed linear space)又稱為賦擬范線性空間,簡稱賦準范空間。...... 賦準范線性空間(paranormed linear space)又稱為賦擬范線性空間,簡稱賦...
在通常的套用中,例如在函式空間中,它們有一個代數結構,即構成一個線性空間,同時還與某種收斂性相聯繫,處理這種結構最常用的一般方法是引入一個範數,這樣就導致賦...
賦范線性空間是一類可以引進“長度”概念的線性空間。 一致凸賦范線性空間(uniformly convexnormed linear space)是滿足一致凸性的一類賦范線性空間。 [1] 中文...
嚴格凸賦范線性空間(strictly convex normed linear space)是滿足嚴格凸性的一類賦范線性空間,簡稱為嚴格凸空間,常用於討論最佳逼近元的唯一性,以及有界線性泛函保...
拓撲線性空間是泛函分析的重要分支,又稱之為拓撲向量空間,它是具有拓撲結構的線性空間,是賦范線性空間概念的推廣。20世紀初,法國數學家弗雷歇在引入距離空間,並用...
代數學中的n元向量、矩陣、多項式,分析學中的函式等)的本質屬性後抽象出來的數學概念,近代數學中不少的研究對象,如賦范線性空間、模等都與線性空間有著密切的...
平性凸賦范線性空間(flat convex normed linear space)是一類賦范線性空間。...... 平性凸賦范線性空間(flat convex normed linear space)是一類賦范線性空間。...
,則在‖0‖下,H構成一個線性賦范空間。完備的內積空間稱為希爾伯特空間,希爾伯特空間的概念還可以推廣到復線性空間上。歐幾里德空間是希爾伯特空間的一個重要特例,...
賦范線性空間(normed linear space)是線上性空間中引進一種與代數運算相聯繫的度量,即由向量範數誘導出的度量。賦范線性空間稱為Banach空間,是指由範數導出的度量...
有理數集Q即為整數二元組集合關於以上等價關係~的商集。商集賦范線性空間的商空間 編輯 設X是線性空間,Y是X的一個線性子空間。對x∈X,記 稱 是以x為代表...
強拓撲是一種拓撲。局部凸空間X中原有的拓撲,相對於弱拓撲σ(X,X)稱為X的強拓撲。例如賦范線性空間的強拓撲即為範數拓撲。部凸空間是最重要的一類拓撲線性空間...
設X,Y是兩個賦范線性空間,U是X到Y的映射,若對一切x∈X,有||Ux||=||x||,則稱U是保范映射或等距映射。保范同構定義 如果U不僅保范,而且還是從X到Y上...
範數(norm)是數學中的一種基本概念。在泛函分析中,它定義在賦范線性空間中,並滿足一定的條件,即①非負性;②齊次性;③三角不等式。它常常被用來度量某個向量...
範數拓撲(norm topology)是賦范線性空間中由範數導出的拓撲。在範數拓撲下,收斂的概念即是依範數收斂。...
完備的賦范代數稱為巴拿赫代數(Banach代數),它是泛函分析的一個重要分支,主要研究帶有乘法的賦范線性空間的性質及其套用。...
強制泛函是賦范線性空間中隨著範數的無限增大而一致趨向於無窮大的泛函。...... 強制泛函是賦范線性空間中隨著範數的無限增大而一致趨向於無窮大的泛函。...
設A是賦范線性空間X到賦范線性空間Y的有界線性運算元,如果值域𝓡(A)是Y的有限維線性子空間,則稱A是有限秩運算元。...
《泛函分析講義》是2011年科學出版社出版的圖書,作者是黎永錦。該書講述了度量空間、賦范線性空間、有界線性運算元等方面的知識。...
等價範數(equivalence of norms)是同一個線性空間上的兩個範數之間的一種關係。有限維空間上的任何兩個範數必是等價的,且具有相同維數的兩個有窮維線性賦范空間...
