基本介紹
- 中文名：桶型空間
- 外文名：barreled space
- 領域：數學
- 性質：局部凸空間
- 集合：桶集
- 充要條件：下半連續的半範數必是連續
概念,拓撲線性空間,局部凸空間,完備空間,範數,半範數,
概念
桶型空間(barreled space)是一類局部凸空間。設E是局部凸空間，E中的吸收的均衡凸閉集稱為桶集。在序列完備空間中，因而在有界完備空間中，桶集吸收每個有界集。如果局部凸空間E的每個桶集都是零元的鄰域，則E稱為桶型空間。E成為桶型空間的充分必要條件是每個下半連續的半範數必是連續的。桶型空間的研究與一致有界定理在拓撲線性空間中的推廣有密切的聯繫。
拓撲線性空間
拓撲線性空間是泛函分析的重要分支，又稱之為拓撲向量空間，它是具有拓撲結構的線性空間，是賦范線性空間概念的推廣。
20世紀初，法國數學家弗雷歇在引入距離空間，並用距離概念來統一過去分析學中的許多重要收斂時，就知道[a，b]上一列函式的“點點收斂”概念是不能用距離收斂來描述的。20世紀30年代以來，泛函分析中大量套用弱收斂、弱拓撲，它們都不能用距離來描述。這就很自然地把賦范線性空間理論發展成更一般的拓撲線性空間理論，其中最主要的成就是局部凸拓撲線性空間理論。這一分支的發展是與一般拓撲學的發展緊密聯繫在一起的。拓撲學方法在這裡發揮了極其重要的作用，法國數學家勒雷和波蘭數學家紹德爾所推廣的不動點定理就是有力的例證之一。1935年以後，經過十多年的努力，這一分支終於形成，它的許多結果不僅在泛函分析中有著廣泛的套用，而且為其他分析學科的深入研究提供了基本框架和有力的工具。
局部凸空間
局部凸空間是最重要的一類拓撲線性空間。設E是拓撲線性空間，如果E中存在由均衡凸集組成的零元的鄰域基，就稱E是局部凸的拓撲線性空間，簡稱局部凸空間，而E的拓撲稱為局部凸拓撲。零元的每個均衡凸鄰域V的閔科夫斯基泛函pV(x)是E上的連續半範數。反之，設{pλ|λ∈Λ}是E上一族半範數，E上使pλ(λ∈Λ)均為連續的最弱拓撲是局部凸的，且零元的均衡凸鄰域基由下面形式的集組成：
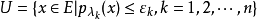
這個局部凸拓撲稱為由半範數族{pλ}確定的局部凸拓撲。如果對任何x∈E(x≠0)，都存在λ∈Λ使pλ(x)≠0，則{pλ|λ∈Λ}確定的局部凸拓撲是豪斯多夫拓撲。通常局部凸空間都指豪斯多夫局部凸空間。E中的定向半序點列{xα}收斂於x∈E等價於對每個λ∈Λ，pλ(xα-x)→0。設E1是由另一半範數族{qβ}確定的局部凸空間，則使線性映射T：E→E1連續的充分必要條件是，對任意的qβ，總存在有限個λ1，λ2，…，λn∈Λ和常數c，使不等式：
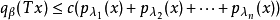
局部凸空間的完備化空間也是局部凸的。根據哈恩-巴拿赫泛函延拓定理，局部凸空間上存在足夠多的非零連續線性泛函。正因為如此，局部凸空間理論成為拓撲線性空間理論中最重要的部分。
完備空間
完備空間或者完備度量空間是具有下述性質的空間：空間中的任何柯西序列都收斂在該空間之內。以有限維空間來說，向量的範數相當於向量的模的長度。但是在有限維歐式空間中還有一個很重要的概念—向量的夾角，特別是兩個向量的正交。內積空間是特殊的線性賦范空間，在這類空間中可以引入正交的概念以及投影的概念，從而在內積空間中建立起相應的幾何學。用內積導出的範數來定義距離，Banach空間就成為了希爾伯特空間。
對任一度量空間M，我們可以構造相應的完備度量空間M'（或者表示為），使得原度量空間成為新的完備度量空間的稠密子空間。M'具備以下普適性質：若N為任一完備度量空間，f為任一從M到N的一致連續函式，則存在唯一的從M'到N的一致連續函式f'使得該函式為f的擴展。新構造的完備度量空間M'在等距同構意義下由該性質所唯一決定，稱為M的完備化空間。
以上定義是基於M是M'的稠密子空間的概念。我們還可以將完備化空間定義為包含M的最小完備度量空間。可以證明，這樣定義的完備化空間存在，唯一（在等距同構意義下），且與上述定義等價。
對於交換環及於其上的模，同樣可以定義相對於一個理想的完備性及完備化。
範數
設E為R上或C上的向量空間。 x→‖x‖為E上的半範數，若E的向量x為零的充分必要條件是‖x‖=0則這個半範數叫做E上的範數。
正實數‖x‖叫做向量x的範數。從E×E到R+中使E之任一向量偶(x，y)對應正實數‖x-y‖的映射d是E上的距離。
對應於範數的距離具有下列兩條性質：
——對E的任一向量偶(x，y)及任一純量α，
d(αx，αy)=|α|·d(x，y)(齊性)；
——對E之向量的任一三元組(x，y，z)，
d(x+z，y+z)=d(x，y)
半範數
半範數是範數的一種推廣。設X是線性空間，p(·)是X上的實值函式，滿足：
1.p(x)≥0(x∈X);
2.p(αx)=|α|p(x)(α為數，x∈X);
3.p(x+y)≤p(x)+p(y)(x，y∈X);
則稱p(x)是x的半範數。通常也將向量x的半範數記為‖x‖，而稱(X，‖·‖)為賦半范線性空間，簡稱賦半范空間。設p(·)是X上的半範數，令E={x|p(x)=0}，則E是X的線性子空間。如果在商空間X/E上規定‖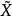
‖=p(x)，則‖·‖是X/E上的範數，稱為由半範數p(·)導出的範數。半範數這個概念在拓撲線性空間理論中扮演著重要的角色，是處理一類特殊凸集的解析工具。
