基本介紹
發展史
定義

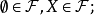




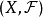


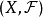


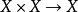
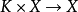

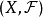
舉例
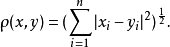
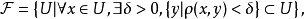
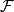

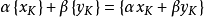

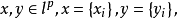
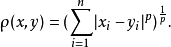
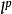
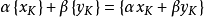
拓展
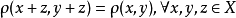
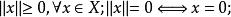
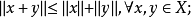
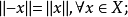
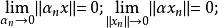
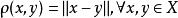










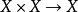
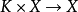

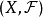
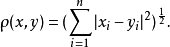
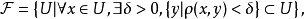
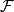

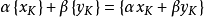

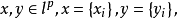
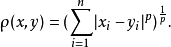
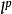
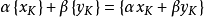
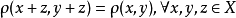
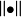
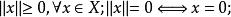
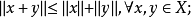
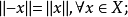
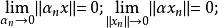
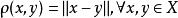
拓撲線性空間理論是泛函分析的一個重要分支,又稱之為拓撲向量空間,它是具有拓撲結構的線性空間,是賦范線性空間概念的推廣。...
模糊拓撲線性空間(fuzzy topological vectorspace)是拓撲線性空間的一種推廣。它是一種帶有與線性結構相適應的模糊拓撲的線性空間。...
本書講述拓撲線性空間的一般理論和它們的某些套用。全書由六章和兩個附錄組成。前面三章敘述拓撲線性空間的基本理論。...
線性拓撲空間,又稱拓撲向量空間或拓撲線性空間。假設X是實(或復)的線性空間,又設x是X上的一個拓撲,如果拓撲空間滿足下列條件,則稱(X,x)為線性拓撲空間:(1)(...
強拓撲是一種拓撲。局部凸空間X中原有的拓撲,相對於弱拓撲σ(X,X)稱為X的強拓撲。例如賦范線性空間的強拓撲即為範數拓撲。部凸空間是最重要的一類拓撲線性空間...
度量線性空間(metric linear space)是一類定義了距離的線性空間。設E是線性空間,又是度量空間,ρ是E上的距離,且E按ρ導出的拓撲成為拓撲線性空間,則稱E為度量...
麥基空間(Mackey space)是一類局部凸空間。設(X,Y)為對偶線性空間,在Y的每個弱緊凸集上一致收斂的拓撲是一種可允許拓撲,稱為X上的麥基拓撲,記為τ(X,Y)。...
核型空間(nuclear space)是一類局部凸空間。局部凸空間是最重要的一類拓撲線性空間。設E是拓撲線性空間,如果E中存在由均衡凸集組成的零元的鄰域基,就稱E是局部凸...
設E和Eα(α∈𝒜)是線性空間,𝓛α是Eα上的分離局部凸拓撲,uα:E→Eα是E到Eα中的線性映射,𝓛是E上使每個線性映射uα(α∈𝒜)都是(E,𝓛)...
則由半範數族{pA(x)|A∈𝒴}確定的X上局部凸拓撲T𝒴,稱為關於對偶線性空間(X,Y)的一個可允許拓撲,或在集類𝒴上的一致收斂拓撲,而相應的有界集族𝒴...
強運算元拓撲(strong operator topology)是運算元空間中的又一種拓撲。從賦范線性空間X到賦范線性空間Y的有界線性運算元全體所成的賦范線性空間B(X→Y)中由半范族{...
局部有界空間是一類拓撲線性空間,如果拓撲線性空間E中存在零元的一個有界的鄰域,則稱E是局部有界的。局部有界空間是亥爾斯(D.H.Hyers)於1939年引入的,局部有...
範數拓撲(norm topology)是賦范線性空間中由範數導出的拓撲。在範數拓撲下,收斂的概念即是依範數收斂。...
1927年和1929年哈恩和巴拿赫先後證明了完備賦范空間上泛函延拓定理,引入了賦范線性空間的對偶空間(當時稱之為極空間),這個定理的推廣形式後來在局部凸拓撲線性空間...
相對內部(relative interior)是指拓撲線性空間中的集合在相對意義下的內部。設A是拓撲線性空間X的子集,A相對其閉仿射包的內部稱為A的相對內部。這個概念在拓撲線性...
泛函分析拓撲線性空間 編輯 由於泛函分析源自研究各種函式空間,在函式空間裡函式列的收斂有不同的類型(譬如逐點收斂,一致收斂,弱收斂等等),這說明函式空間裡有不同...
