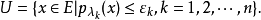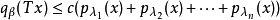弱拓撲(weak topology)是一種局部凸拓撲。設線性空間對(X，Y)關於雙線性泛函〈·，·〉成為對偶，稱X上由半範數族{|〈·，y〉||y∈Y}確定的局部凸拓撲為X的關於對偶Y的弱拓撲，記為σ(X，Y)。
局部凸空間是最重要的一類拓撲線性空間。設E是拓撲線性空間，如果E中存在由均衡凸集組成的零元的鄰域基，就稱E是局部凸的拓撲線性空間，簡稱局部凸空間，而E的拓撲稱為局部凸拓撲。
基本介紹
- 中文名：弱拓撲
- 外文名：weak topology
- 領域：數學
- 性質：局部凸拓撲
- 空間：局部凸空間
- 相對概念：強拓撲
概念,拓撲,局部凸空間,賦范線性空間,拓撲線性空間,
概念
弱拓撲(weak topology)是一種局部凸拓撲。設線性空間對(X，Y)關於雙線性泛函〈·，·〉成為對偶，稱X上由半範數族{|〈·，y〉||y∈Y}確定的局部凸拓撲為X的關於對偶Y的弱拓撲，記為σ(X，Y)。對稱地，Y上由半範數族{|〈x，·〉||x∈X}確定的局部凸拓撲稱為Y的關於對偶X的弱拓撲，記為σ(Y，X)。當X為局部凸空間時，(X，X)為自然對偶，σ(X，X)稱為X的弱拓撲，而σ(X，X)稱為X的弱*拓撲。相應地，X中原有的拓撲稱為強拓撲。一般地，X的弱拓撲比強拓撲弱，從而弱閉集必是強閉集；對於凸集，其逆也成立，即強閉凸集也是弱閉的.集合的弱有界性與強有界性是等價的。
拓撲
1.X與空集都屬於T;
2.T中任意兩個成員的交屬於T;
3.T中任意多個成員的並屬於T;
則T稱為X上的一個拓撲。具有拓撲T的集合X稱為拓撲空間，記為(X，T)。
設T1與T2為集合X上的兩個拓撲。若有關係T1T2，則稱T1粗於T2，或T2細於T1。當X上的兩個拓撲相互之間沒有包含關係時，則稱它們是不可比較的。在集合X上，離散拓撲是最細的拓撲，平凡拓撲是最粗的拓撲。
局部凸空間
局部凸空間是最重要的一類拓撲線性空間。設E是拓撲線性空間，如果E中存在由均衡凸集組成的零元的鄰域基，就稱E是局部凸的拓撲線性空間，簡稱局部凸空間，而E的拓撲稱為局部凸拓撲。零元的每個均衡凸鄰域V的閔科夫斯基泛函pV(x)是E上的連續半範數.反之，設{pλ|λ∈Λ}是E上一族半範數，E上使pλ(λ∈Λ)均為連續的最弱拓撲是局部凸的，且零元的均衡凸鄰域基由下面形式的集組成：
這個局部凸拓撲稱為由半範數族{pλ}確定的局部凸拓撲。如果對任何x∈E(x≠0)，都存在λ∈Λ使pλ(x)≠0，則{pλ|λ∈Λ}確定的局部凸拓撲是豪斯多夫拓撲.通常局部凸空間都指豪斯多夫局部凸空間.E中的定向半序點列{xα}收斂於x∈E等價於對每個λ∈Λ，pλ(xα-x)→0.設E1是由另一半範數族{qβ}確定的局部凸空間，則使線性映射T：E→E1連續的充分必要條件是，對任意的qβ，總存在有限個λ1，λ2，…，λn∈Λ和常數c，使不等式：
對一切x∈E成立。
局部凸空間的完備化空間也是局部凸的。根據哈恩-巴拿赫泛函延拓定理，局部凸空間上存在足夠多的非零連續線性泛函。正因為如此，局部凸空間理論成為拓撲線性空間理論中最重要的部分。
賦范線性空間
賦范線性空間是一類可以引進“長度”概念的線性空間。設X是線性空間，X上滿足下列條件的實值函式p(·)稱為X上的範數：
1.p(x)≥0(x∈X);p(x)=0⇔x=0.
2.p(αx)=|α|p(x)(α為數，x∈X).
3.p(x+y)≤p(x)+p(y)(x，y∈X).
對x∈X，p(x)稱為x的範數，通常記為‖x‖.賦有範數的線性空間(X，‖·‖)稱為賦范線性空間，簡稱賦范空間。
拓撲線性空間
拓撲線性空間是一類具有拓撲結構的線性空間。如果實數域或複數域K上的線性空間E同時是有拓撲τ的拓撲空間，並且線性空間的基本運算x+y和αx(x，y∈E，α∈K)分別作為E×E和K×E到E中的映射按τ是連續的，則稱E為(實或復)拓撲線性空間或拓撲向量空間。而τ稱為E的線性拓撲或向量拓撲，零元的均衡的鄰域全體組成零元的鄰域基。滿足T1分離公理的拓撲線性空間是完全正則的。
