相對化拓撲

在拓撲學和數學的其他相關領域裡，拓撲空間 X 的子空間是指在 X 中子集 S 及在 S 上賦予的由 X 的拓撲所誘導的拓撲．這個誘導出來的拓撲叫做 X 的拓撲在 S 上的相對化拓撲，也叫子空間拓撲、“自然拓撲”．

基本介紹

• 中文名：相對化拓撲
• 分類：數理科學

定義

給定一拓撲空間 (X,τ) 和一 X 內的子集 S ，於 S 上的子空間拓撲被定義為

亦即， S 的子集於子空間拓撲中為開集若且唯若其為 S 和一於 (X,τ) 內的開集的交集。若 S 被設上子空間拓撲，則其本身即為一拓撲空間，並被稱之為 (X,τ) 的子空間。除非有額外敘述，一般拓撲空間的子集都會假定設有一子空間拓撲。

若 S 為 (X,τ) 內的開集、閉集或稠密集，則分別稱 (S,τS) 為 (X,τ) 內的一開子空間、閉子空間或稠密子空間。

另外，也可以定義 X 內的子集 S 的子空間拓撲為會使得內含映射

為連續的最弱拓撲。

更一般地，設 i 為一由集合 S 至拓撲空間 X 的單射，則於S上的子空間拓撲即為定義為 i 為連續的最弱拓撲。此拓撲的開集恰好會是 i(U) 的其中一個，其中的 U 為 X 內的開集。 S 因此同胚於在 X 內的值域（也是帶子空間拓撲），且 i 會被稱之為拓撲嵌入。

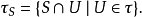
例子

• 給定一具一般拓撲的實數，其自然數（實數的一子空間）的子空間拓撲會是一個離散拓撲。
  
• 有理數Q做為一個R的子空間，不帶有離散拓撲（點 0 在Q內不是開集）。
  
• 令S= [0,1) 為實線R的一子空間，則 [0,½) 在S內為開集，但在R內則不是。相似地，[½, 1) 在S內為閉集，但在R內則不是。S為其自身的開子集和閉子集，但做為R的子集則兩者皆不是。