通常拓撲(usual topology)是一類特殊的拓撲。設Rn為n維歐幾里得空間,Rn中按歐幾里得空間的度量確定的拓撲在X上的相對拓撲稱為X上的通常拓撲。
基本介紹
- 中文名:通常拓撲
- 外文名:usual topology
- 領域:數學
- 學科:拓撲學
- 性質:一類特殊的拓撲
- 特點:仿緊、局部連通
概念
拓撲
歐幾里得空間
性質
分離公理
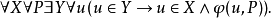


通常拓撲(usual topology)是一類特殊的拓撲。設Rn為n維歐幾里得空間,Rn中按歐幾里得空間的度量確定的拓撲在X上的相對拓撲稱為X上的通常拓撲。
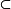
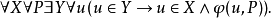

通常拓撲(usual topology)是一類特殊的拓撲。設Rn為n維歐幾里得空間,Rn中按歐幾里得空間的度量確定的拓撲在X上的相對拓撲稱為X上的通常拓撲。...
一般拓撲學(geoneral topology)是用點集的方法研究拓撲不變數的拓撲分支。它的前身是點集拓撲學。 一般拓撲學的歷史約六十年,由於它適應了科學的發展,其生命力是...
拓撲學(topology),是研究幾何圖形或空間在連續改變形狀後還能保持不變的一些性質的學科。它只考慮物體間的位置關係而不考慮它們的形狀和大小。在拓撲學裡,重要的...
《一般拓撲學基礎》是2012-9出版的圖書,作者是張德學。...... 張德學編著的《一般拓撲學基礎》是為本科生編寫的一般拓撲學教材,主要介紹一般拓撲學中最基本的概念和...
《一般拓撲學》是關於一般拓撲的一部經典著作。...... 書中系統地介紹了一般拓撲的基本知識。正文共分七章,包括拓撲空間、Moore-Smith收斂、乘積空間和商空間、嵌入...
對一個有向無環圖(Directed Acyclic Graph簡稱DAG)G進行拓撲排序,是將G中所有頂點排成一個線性序列,使得圖中任意一對頂點u和v,若邊(u,v)∈E(G),則u線上...
拓撲結構是指網路中各個站點相互連線的形式,在區域網路中明確一點講就是檔案伺服器、工作站和電纜等的連線形式。現在最主要的拓撲結構有匯流排型拓撲、星形拓撲、環形...
初拓撲,在一般拓撲學與數學的相關領域中,給定集合X與集合X上的一族函式,其初拓撲(theinitialtopology)是使得這一族函式連續的最粗的拓撲。拓撲子空間與乘積空間都...
拓撲結構圖是指由網路節點設備和通信介質構成的網路結構圖。 在選擇拓撲結構時,主要考慮的因素有:安裝的相對難易程度、重新配置的難易程度、維護的相對難易程度、...
在數學裡,拓撲分析,即拓撲學(英語:topology),或意譯為位相幾何學,是一門研究拓撲空間的學科,主要研究空間內,在連續變化(如拉伸或彎曲,但不包括撕開或黏合)下...
點集拓撲學(Point Set Topology),有時也被稱為一般拓撲學(General Topology),是數學的拓撲學的一個分支。它研究拓撲空間以及定義在其上的數學結構的基本性質。這...
緊補拓撲(compact complement topology)一種拓撲結構.在實數集R上,由緊集的補集及空集構成的拓撲稱為R上的緊補拓撲,相應的拓撲空間稱為緊補空間.緊補拓撲粗於R...
