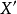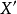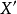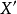局部凸空間X為半蒙泰爾空間是指:如果X中的每一個有界集是相對緊的。半蒙泰爾空間且是桶式的稱為蒙泰爾(Montel)空間。蒙泰爾空間(Montel space)是一類桶型空間。如果桶型空間E的任意有界閉集都是緊的,則稱它為蒙泰爾空間或M空間。M空間是自反的,其共扼空間也是M空間。蒙泰爾空間是廣義函式論中十分有用的一類空間。
基本介紹
- 中文名:蒙泰爾空間
- 外文名:Montel Space
- 套用學科:數學術語
- 範疇:數理科學
- 定義:一類桶型空間
- 又稱:Montel空間
概念,基本原理,
概念
局部凸空間X為半蒙泰爾空間是指:如果X中的每一個有界集是相對緊的。半蒙泰爾空間且是桶式的稱為蒙泰爾(Montel)空間。蒙泰爾空間(Montel space)一類桶型空間。如果桶型空間E的任意有界閉集都是緊的,則稱它為蒙泰爾空間或M空間。M空間是自反的,其共扼空間也是M空間。蒙泰爾空間是廣義函式論中十分有用的一類空間。
基本原理
定理1:對於局部凸空間 ,下述條件是等價的:
,下述條件是等價的:

(a) 中的每個有界集是完全有界集;
中的每個有界集是完全有界集;

(b)在 中的每個有界集
中的每個有界集 上,
上, 和
和 一致;
一致;




(c) 中的每個等度連續集合
中的每個等度連續集合 按強拓撲
按強拓撲 是相對緊的(或是完全有界的);
是相對緊的(或是完全有界的);



(d)在 中的每個等度連續集合
中的每個等度連續集合 上,
上, 和
和 一致。
一致。




定理1的證明: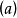 ⇒
⇒ :由
:由 ,
, 上的強拓撲
上的強拓撲 和完全有界集上的一致收斂拓撲
和完全有界集上的一致收斂拓撲 是一致的。在
是一致的。在 中每個等度連續集合
中每個等度連續集合 上,
上, 和
和 是一致的。
是一致的。
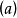




























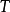
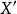







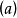



定理2: 空間
空間 的強對偶
的強對偶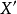 是蒙泰爾空間。
是蒙泰爾空間。


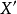
定理2的證明:因為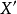 是自反空間,
是自反空間,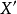 是桶式空間,並且
是桶式空間,並且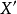 中的每個有界集是等度連續集合,所以知道
中的每個有界集是等度連續集合,所以知道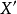 中的每個有界集是相對緊的,即知
中的每個有界集是相對緊的,即知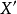 是蒙泰爾空間。
是蒙泰爾空間。