在數學中,等距同構是指在度量空間之間保持距離關係的同構。幾何學中的對應概念是全等變換。
令(N,ρ)、(N1,ρ1)表示兩個度量空間,如果存在一個映射φ:N→N1滿足如下條件:
1)φ為滿射;
2)ρ(x,y)=ρ1(φ(x),φ(y))(∀x,y∈N),
則認為空間(N,ρ)和空間(N1,ρ1)是等距同構的。
基本介紹
- 中文名:等距同構
- 外文名:isometry
- 所屬領域:數理科學
- 分類:正交運算元、酉運算元
- 套用範圍:實內積空間和復內積空間
定義
 式1
式1 式2
式2 式3
式3 式4
式4相關性質與定理
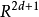

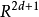


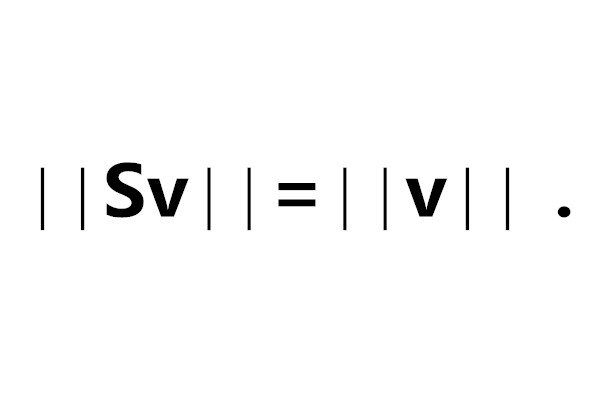
在數學中,等距同構是指在度量空間之間保持距離關係的同構。幾何學中的對應概念是全等變換。
令(N,ρ)、(N1,ρ1)表示兩個度量空間,如果存在一個映射φ:N→N1滿足如下條件:
1)φ為滿射;
2)ρ(x,y)=ρ1(φ(x),φ(y))(∀x,y∈N),
則認為空間(N,ρ)和空間(N1,ρ1)是等距同構的。
 式1
式1 式2
式2 式3
式3 式4
式4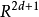

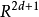


在數學中,等距同構是指在度量空間之間保持距離關係的同構。幾何學中的對應概念是全等變換。令(N,ρ)、(N1,ρ1)表示兩個度量空間,如果存在一個映射φ:N→N1...
如果空間X,Y之間存在一個保范同構映射,就稱X與Y保范同構,亦稱等距同構。...... 如果空間X,Y之間存在一個保范同構映射,就稱X與Y保范同構,亦稱等距同構。...
這個定理建立了希爾伯特空間與它的對偶空間的一個重要聯繫:如果底域是實數,兩者是等距同構;如果域是複數,兩者是等距反同構。在泛函分析中有多個有名的定理冠以里斯...
它是等距同構,是仿射空間中仿射變換的一種。它可以視為將同一個向量加到每點上,或將坐標系統的中心移動所得的結果。即是說,若是一個已知的向量,是空間中一點...
在物理學與數學上,龐加萊群(英語:Poincaré group)是狹義相對論中閔可夫斯基時空的等距同構群,由赫爾曼·閔可夫斯基引進,龐加萊群是以法國數學家亨利·龐加萊...
一個物件(如一維、二維或三維中的圖像或信號)的對稱群是指在複合函式運算下不變的所有等距同構所構成的群。其為所考慮之空間的等距同構群中的一個子群。(若沒...
對於度量空間R,如果有完備的度量空間R,使R等距同構於R1的一個稠密子空間,則稱R1是R的完備化空間。任何度量空間都必存在完備化空間,且若除去等距同構不計外,完備...
卷結群和壁紙群是歐幾里德平面的等距同構群的離散子群。壁紙群是餘緊緻的,但卷結群不是。空間群是某維度的歐幾里德空間的等距同構群的離散子群。...
詹姆斯空間是詹姆斯(James,R.C.) 於1951年針對當時關於“巴拿赫空間X等距同構於X**推出X必自反”的猜測而構造的空間。...
設X是巴拿赫空間,如果任何可分的巴拿赫空間都等距同構於X的某個閉子空間,則X稱為萬有空間,亦稱X具有萬有性。...
F的基數稱為希爾伯特空間H的維數。兩個維數相同的希爾伯特空間是等距同構的。規範正交基實際上是歐幾里得空間中規範正交基的一種推廣。...
