基本介紹
- 中文名：規範正交基
- 外文名：orthonormal basis
- 學科：線性代數
- 適用條件：歐幾里得空間
- 性質：都是單位向量並且彼此正交
- 相似名詞：正交基
簡介,舉例,基本式,不完全正交基,存在性,
簡介
在數學中，特別是線性代數，具有有限維度的內積空間V的正交基是其向量的基，即它們都是單位向量並且彼此正交。例如，歐幾里德空間Rn的標準基是正交基，其中內積是向量的點積。在旋轉或反射（或任何正交變換）下的標準基的映射也是正交的，並且Rn的每個正交基都以這種形式出現。
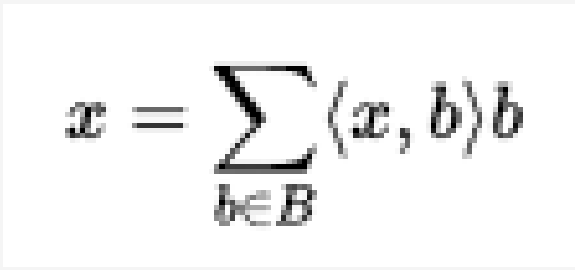
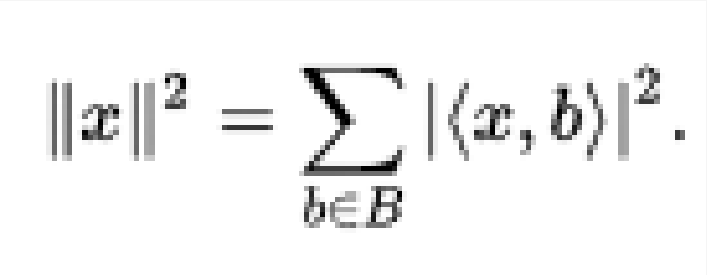
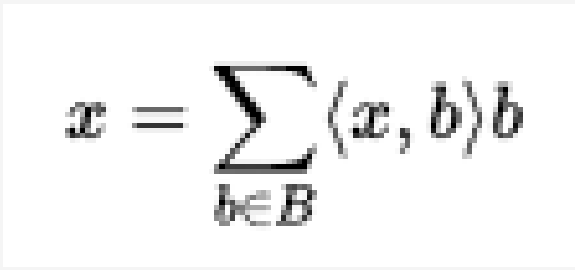
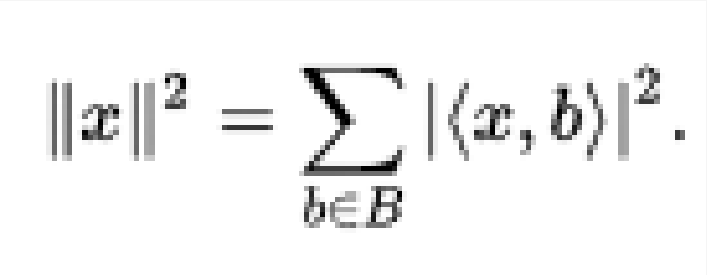
規範正交基(orthonormal basis)完備的規範正交系。設H為希爾伯特空間，H的完備的規範正交系F稱為H的規範正交基或正規正交基。F的基數稱為希爾伯特空間H的維數。兩個維數相同的希爾伯特空間是等距同構的。規範正交基實際上是歐幾里得空間中規範正交基的一種推廣。
對於一般的內積空間V，可以使用正交基數來定義V上的歸一化正交坐標。在這些坐標下，內積變為向量的點積。因此，正交基的存在減少了有限維內部空間的研究，以研究點陣積分下的Rn。每個有限維的內積空間都有一個正交基，這可以從任意的基礎上使用格拉姆 - 施密特方法獲得。
在功能分析中，正交基的概念可以推廣到任意（無限維）內積空間（或希爾伯特前空間）。給定希爾伯特前空間H，H的正交基是正交的向量集合，其特徵在於H中的每個向量可以被寫為基於向量的無限線性組合。在這種情況下，正交基礎有時被稱為H的希爾伯特基。注意，在這個意義上，正交基通常不是哈默爾基礎，因為需要無限線性組合。具體來說，基礎的線性跨度必須在H中是緻密的，但它可能不是整個空間。
如果我們進入希爾伯特空間，那么與正交基數相同的線性跨度的非正交矢量集合可能根本不是基。例如，間隔[-1,1]上的任何平方可積分函式可以被表示（幾乎在任何地方）作為勒布雷多項式的無限和（一個獨立基礎），但不一定作為單項式xn的無限和。
舉例
向量集合{e1 =（1,0,0），e2 =（0,1,0），e3 =（0,0,1）}（標準基）形成R3的正交基。
證明：一個簡單的計算表明，這些向量的內積等於零，⟨e1，e2⟩=⟨e1，e3⟩=⟨e2，e3⟩= 0，它們的維度都等於1，|| e1 || = || e2 || = || e3 || = 1。這意味著{e1，e2，e3}是正交集合。 R3中的所有向量（x，y，z）可以表示為基向量的和：
所以{e1，e2，e3}一定是R3的基。還可以表明，圍繞軸線穿過原點旋轉或者通過原點反射的平面的標準基礎形成R3的正交基。
基本式
如果B是H的正交基，則H的每個元素x可以被寫為
當B是正交的時候，這就簡化成
x的範數的平方可以給出
即使B是不可數的，這個總和中很多是非零的，因此表達式是明確的。 這個總和也稱為x的傅立葉擴展，公式通常稱為Parseval的身份。
不完全正交基
給定希爾伯特空間H和H中相互正交向量的集合S，我們可以取包含S的H的最小閉合線性子空間V，然後S將是V的正交基；當它是一個完整的正交集合時，其當然可以小於H本身，是不完整的正交集，或者是H。
存在性
使用Zorn的引理和Gram-Schmidt過程（或更簡單的排序順序和無限次遞歸），可以顯示每個希爾伯特空間都承認了一個基礎，從而得到了一個正交基礎；此外，相同空間的任何兩個正交基座具有相同的基數（這可以以類似於向量空間的通常維度定理的證明的方式被證明，並且取決於較大的基礎候選是可數的還是單獨的情況） 不）。 若且唯若它承認可數的正交基礎時，希爾伯特空間是可分離的。 （可以證明這最後一個陳述，而不使用公理的選擇）
