C2類運算元稱為希爾伯特-施密特運算元,而相應的範數‖·‖2稱為希爾伯特-施密特範數。
基本介紹
- 中文名:希爾伯特-施密特範數
- 外文名:Hilbert-Schmidt norm
- 適用範圍:數理科學
簡介
施凱特p類運算元




定義





性質
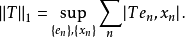




C2類運算元稱為希爾伯特-施密特運算元,而相應的範數‖·‖2稱為希爾伯特-施密特範數。









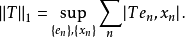




C2類運算元稱為希爾伯特-施密特運算元,而相應的範數‖·‖2稱為希爾伯特-施密特範數。...... C2類運算元稱為希爾伯特-施密特運算元,而相應的範數‖·‖2稱為希爾伯特-施密特...
希爾伯特-施密特積分運算元(Hilbert-Schmidtintegral operator)是一類核平方可積的積分型運算元。...
C2類運算元稱為希爾伯特-施密特運算元,而相應的範數‖·‖2稱為希爾伯特-施密特範數。...... C2類運算元稱為希爾伯特-施密特運算元,而相應的範數‖·‖2稱為希爾伯特-施密特...
索伯列夫空間是賦范線性空間,在以下範數下其為巴拿赫空間:若 ,該空間往往記為 ,我們使用 表示該空間因為此時索伯列夫空間為希爾伯特空間。...
是跡類運算元空間上的內積;相應的範數被稱為希爾伯特-施密特範數。 跡類運算元在希爾伯特-施密特範數意義下的完備化被稱為希爾伯特-施密特運算元。...
對希爾伯特-施密特運算元,以它奇異數平方和的平方根作範數,也成為一個希爾伯特空間,這時內積(T,S)=tr(T)。全連續運算元卡金代數 編輯 全連續運算元類有一個重要的代數...
酉膨脹是將某一希爾伯特空間上的運算元按一定條件膨脹為另一更大的希爾伯特空間上...壓縮運算元是對任何點的範數都不放大的一類線性運算元,又稱為收縮運算元。收縮運算元在...
20世紀以來,當人們研究了許多具體的無限維空間及其上面相應的收斂性以後,自然而然地轉向抽象形態的線性空間以及按範數收斂的概念。德國數學家希爾伯特、法國數學家...
20世紀以來,當人們研究了許多具體的無限維空間及其上面相應的收斂性以後,自然而然地轉向抽象形態的線性空間以及按範數收斂的概念。德國數學家希爾伯特、法國數學家...
20世紀以來,當人們研究了許多具體的無限維空間及其上面相應的收斂性以後,自然而然地轉向抽象形態的線性空間以及按範數收斂的概念。德國數學家希爾伯特、法國數學家...
3.2.2 範數的等價性 623.2.3 有限維線性賦范空間的性質 623.3 內積空間與希爾伯特空間 653.3.1 內積與內積空間 653.3.2 正交與正交分解 683.4 內積...
包括10章內容,分別是變分法、希爾伯特空間、二階線性常微分方程、貝塞爾函式、狄拉克δ函式、格林函式、範數、積分方程、數論在物理逆問題中的套用和任意維空間的...
他1918年去哥廷根大學從D.希爾伯特、E.G.H.蘭道、(A.)E.諾特、E.赫克...並以同樣的精神處理代數數論問題,證明範數定理,進而於1931年同E.諾特和R.(D....
在代數數域中,他研究了對於冪剩餘記號的互反律、範數剩餘及其記號、希爾伯特範數記號、代數數域的算術等課題。還以他的名字命名了一種 一函式。1937年第二次世界...
