基本介紹
- 中文名:規範正交基
- 外文名:orthonormal basis
- 學科:線性代數
- 適用條件:歐幾里得空間
- 性質:都是單位向量並且彼此正交
- 相似名詞:正交基
簡介,舉例,基本式,不完全正交基,存在性,
簡介
在數學中,特別是線性代數,具有有限維度的內積空間V的正交基是其向量的基,即它們都是單位向量並且彼此正交。例如,歐幾里德空間Rn的標準基是正交基,其中內積是向量的點積。在旋轉或反射(或任何正交變換)下的標準基的映射也是正交的,並且Rn的每個正交基都以這種形式出現。
規範正交基(orthonormal basis)完備的規範正交系。設H為希爾伯特空間,H的完備的規範正交系F稱為H的規範正交基或正規正交基。F的基數稱為希爾伯特空間H的維數。兩個維數相同的希爾伯特空間是等距同構的。規範正交基實際上是歐幾里得空間中規範正交基的一種推廣。
對於一般的內積空間V,可以使用正交基數來定義V上的歸一化正交坐標。在這些坐標下,內積變為向量的點積。因此,正交基的存在減少了有限維內部空間的研究,以研究點陣積分下的Rn。每個有限維的內積空間都有一個正交基,這可以從任意的基礎上使用格拉姆 - 施密特方法獲得。
在功能分析中,正交基的概念可以推廣到任意(無限維)內積空間(或希爾伯特前空間)。給定希爾伯特前空間H,H的正交基是正交的向量集合,其特徵在於H中的每個向量可以被寫為基於向量的無限線性組合。在這種情況下,正交基礎有時被稱為H的希爾伯特基。注意,在這個意義上,正交基通常不是哈默爾基礎,因為需要無限線性組合。具體來說,基礎的線性跨度必須在H中是緻密的,但它可能不是整個空間。
如果我們進入希爾伯特空間,那么與正交基數相同的線性跨度的非正交矢量集合可能根本不是基。例如,間隔[-1,1]上的任何平方可積分函式可以被表示(幾乎在任何地方)作為勒布雷多項式的無限和(一個獨立基礎),但不一定作為單項式xn的無限和。
舉例
向量集合{e1 =(1,0,0),e2 =(0,1,0),e3 =(0,0,1)}(標準基)形成R3的正交基。
證明:一個簡單的計算表明,這些向量的內積等於零,⟨e1,e2⟩=⟨e1,e3⟩=⟨e2,e3⟩= 0,它們的維度都等於1,|| e1 || = || e2 || = || e3 || = 1。這意味著{e1,e2,e3}是正交集合。 R3中的所有向量(x,y,z)可以表示為基向量的和:

所以{e1,e2,e3}一定是R3的基。還可以表明,圍繞軸線穿過原點旋轉或者通過原點反射的平面的標準基礎形成R3的正交基。
基本式
如果B是H的正交基,則H的每個元素x可以被寫為
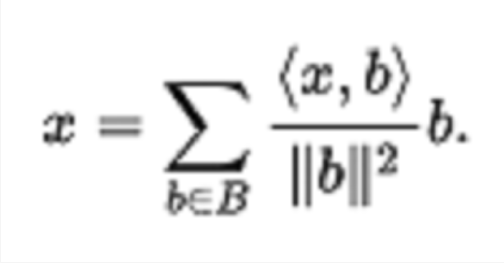
當B是正交的時候,這就簡化成
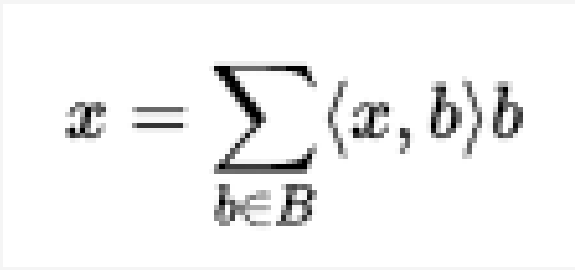
x的範數的平方可以給出
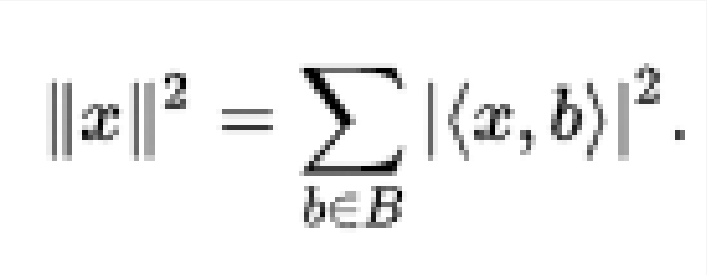
即使B是不可數的,這個總和中很多是非零的,因此表達式是明確的。 這個總和也稱為x的傅立葉擴展,公式通常稱為Parseval的身份。
不完全正交基
給定希爾伯特空間H和H中相互正交向量的集合S,我們可以取包含S的H的最小閉合線性子空間V,然後S將是V的正交基;當它是一個完整的正交集合時,其當然可以小於H本身,是不完整的正交集,或者是H。
存在性
使用Zorn的引理和Gram-Schmidt過程(或更簡單的排序順序和無限次遞歸),可以顯示每個希爾伯特空間都承認了一個基礎,從而得到了一個正交基礎;此外,相同空間的任何兩個正交基座具有相同的基數(這可以以類似於向量空間的通常維度定理的證明的方式被證明,並且取決於較大的基礎候選是可數的還是單獨的情況) 不)。 若且唯若它承認可數的正交基礎時,希爾伯特空間是可分離的。 (可以證明這最後一個陳述,而不使用公理的選擇)
